Question 1155777: 1.) The talent show committee sold a total of 530 tickets in advance. Student tickets cost
$3 each and the adult tickets cost $4 each. If the total receipts were $1740, how many
each type of ticket were sold?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52788)   (Show Source):
You can put this solution on YOUR website! .
Let x be the number of adult tickets; then the number of student tickets is (530-x).
The money equation is
4x + 3*(530-x) = 1740.
From the equation, express x and calculate
x = 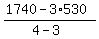 = 150.
ANSWER. 150 adult tickets and (530-150) = 380 student tickets.
CHECK. 150*4 + 380*3 = 1740 dollars. Ok
Solved.
-----------------
It is a standard tickets problem.
There are different methods of solving such problems.
In this site, there are lessons
- Using systems of equations to solve problems on tickets
- Three methods for solving standard (typical) problems on tickets
explaining and showing all basic methods of solving such problems.
From these lessons, learn on how to solve such problems once and for all.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here's a quick and easy mental solution, if a formal algebraic solution is not required.
530 student tickets at $3 each would make $1590; the actual total is $1740, which is $150 more.
Each adult ticket costs $1 more than each student ticket. To make the additional $150 and keep the total number of tickets the same, trace 1 student ticket for 1 adult ticket 150 times.
ANSWER: 150 adult tickets, which means 380 student tickets.
|
|
|
