|
Question 1155750: Aβ sparkling-water distributor wants to make up 400 gal of sparkling water to sell for $ 8.00 per gallon. She wishes to mix three grades of water selling for β$14β.00, β$3β.00, andβ $4.50 perβ gallon, respectively. She must use twice as much of theβ $4.50 water as the $ 3.00 comma water. How many gallons of each should sheβ use?
Found 3 solutions by josmiceli, ikleyn, greenestamps:
Answer by josmiceli(19441)   (Show Source):
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
This problem is, actually, can be solved using one single equation for one unknown.
Let x = the amount (the volume) of the $3 grade water, in gallons.
Then the amount of the $4.50 grade water is 2x gallons,
and the amount of the $14 grade water is the rest (400 - x - 2x) = (400-3x) gallons.
The money equation is
3x + 4.50*(2x) + 14*(400-3x) = 8*400 dollars.
Simplify and solve for x
3x + 9x + 14*400 - 42x = 8*400
-30x = 8*400 - 14*400
x = 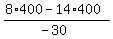 = 80.
ANSWER. 80 gallons of the $3 grade water; 2*80 = 160 gallons of the $4.50 grade water
and the rest, (400-80-160) = 160 gallons of the $14 grade water.
CHECK. 3*80 + 160*4.50 + 14*160 = 3200 dollars, same as 8*400 = 3200 dollars. ! Precisely correct !
Solved.
-----------------
At this site, there is a SPECIAL LESSON explaining and showing how to solve different similar problems in the same way
- Advanced word problems to solve using a single linear equation
-----------------
+-------------------------------------------------------+
| THIS ADDITION IS TO ALL OTHER TUTORS AT THIS FORUM |
+-------------------------------------------------------+
My older grandson is now a second year Stanford university student.
Couple of weeks ago I gave him similar problem, that came to the forum.
My goal was to check if he knows this method (reducing to single equation in one unknown).
Surely, he easily solved the problem. What is MORE INTERESTING, he solved it using EXACTLY THIS METHOD.
I then asked him, if the Math teacher explained this method to them in his school.
"YES", he answered, "in my 6-th or 7-th grade".
He was at a regular middle school that time.
I, at my same age, was also touched to this method (although in other country).
So now I am 179% sure/confident that it is exactly the method to teach the students of this grade.
(Before I was only 129% sure).
-----------------
Similar problems came MANY TIMES to this forum.
Many times I explained here, at the forum, the method of their solution.
I do not think that my solutions went out of you . . .
Surely, we live in the democratic country, and I can not dictate to you on how present your solutions to the forum
(UNFORTUNATELY :)
But when you teach the students differently, you simply miss an opportubity to teach them in a right way (!)
Please keep it in mind (!)
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
If you solve the problem using formal algebra, then certainly use a single variable -- it is MUCH less work.
I solve this kind of problem informally, if I can. The numbers in this problem make it easy; being good with mental arithmetic, I solved the problem in about 15 seconds.
Work with two ingredients at a time, as follows....
The mixture uses twice as much $4.50 water as $3 water. That means the average price of those two ingredients is "twice as close to $4.50 as it is to $3"; that makes the average cost of those two ingredients $4.
Now the problem is to mix $4 water and $14 water to get $8 water.
$8 is 4/10=2/5 of the way from $4 to $14; that means 2/5 of the total mixture is the $14 water.
So 2/5 of the 400 gallons, or 160 gallons, is the $14 water.
That leaves 240 gallons of the $3 water and $4.50 water. Since the amount of $4.50 water is twice the amount of $3 water, that means 160 gallons of the $4.50 water and 80 gallons of the $3 water.
ANSWER:
160 gallons of $14 water
160 gallons of $4.50 water
80 gallons of $3 water
|
|
|
| |
