Question 1155433: a bridge is built in the shape of a parabolic arch. the bridge has a span of 184 ft. and a maximum height of 40 ft. find the height of the arch at 15 ft. from its center
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
Let the center of the arch at ground level be the origin of a coordinate system. Then the parabola passes through the points (-92,0), (0,40), and (92,0).
With the y-intercept at (0,40), the equation is of the form  .
Use the point (92,0) to determine the value of a to complete the equation.
The equation of the parabola is
Evaluate y when x=15 to find the answer to the problem.
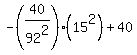 = 38.936673 to several decimal places.
Here is a way to find this value without finding the equation of the parabola.
The basic form of the equation of a parabola is  .
This equation tells us directly that the vertical displacement is proportional to the square of the horizontal displacement.
We know, from the points (0,40) and (92,0) on the parabola, that the vertical displacement is -40 for a horizontal displacement of 92.
The question asks for the height of the bridge 15 feet from the center; we can find that height by determining the vertical displacement from the vertex at (0,40) for a horizontal displacement of 15 from the vertex.
The ratio of horizontal displacements for the two points is 15/92; the ratio of the vertical displacements will be the square of that. So the vertical displacement 15 feet from the center of the arch is
and so the height of the arch 15 feet from its center is 40-1.063327 = 38.936673 feet.
|
|
|
