Question 1155272: List all rational zeros that are possible according to the Rational Zero Theorem
The following function is given: f(X)=x3-5x2-4x+20
I am assuming that I look for the leading coefficient first
Then possible rational zeros Factors of the constant terms
Factors of the leading coefficient
I am going to assume that the constant term is 20.
The leading Coefficient would be 1, 5,-5,2-2,4.-4,20, -20
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!

the Rational Zero Theorem tells us that if  is a zero of is a zero of  , then , then  is a factor of is a factor of  and and  is a factor of is a factor of  . .
The factors of  are ± are ± and and
the factors of  are ± are ± ,± ,±  , ± , ± , ± , ± ,± ,± ,± ,± . .
The possible values for  are: are:
± , ± , ± , ± , ± , ± , ± ,± ,± ,± ,±
These are the  rational zeros for the function. rational zeros for the function.
We can determine which of the possible zeros are 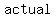 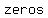 by substituting these values for by substituting these values for  in in  . .
do it and you will see that 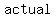 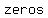 are: are:



Answer by ikleyn(52873)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In your list, you missed -1, 10 and - 10.
Notice, that in your problem, the leading coefficient is 1 (one, ONE), and it makes the solution much EASIER.
The better way is to present your list in this form
+/-1, +/-2, +/-4, +/-5, +/-10, +/-20.
When you present in this form, you are (almost) guaranteed from missing the terms.
------------------
Notices and guidelines
In this problem, the leading coefficient is 1 (at x^3).
The constant term is 20.
You must list all the numbers +/- 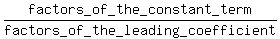 . .
IGNORE THE POST BY @MathLover1, since she presented TOTALLY WRONG solution.
Ignore it for your safety (!) (!) (!)
Dear @MathLover1, in my view, it is ABSOLUTELY INAPPROPRIATE for a tutor to consult students/visitors
in a level as you did it in this case (and in many other cases I observed).
I know that you are able to consult satisfactory/successfully on many simple level problems.
Do it in those areas/topics, where you are confident, and do not go outside, where you have no enough knowledge/expertise.
One more advise: CHECK yourself, using both the formal checks and the common sense.
|
|
|