Question 1155116: There are three boxes containing black and white balls. Box 1 contain 4 white ball, 2 black ball, Box 2 contain 3 white ball and 2 black and Box 3 contain 1 white ball and 2 black. Draw a ball from box 1 and place it in box 2. Then draw a ball from box 2 and place it in box 3. Finally draw a ball from box 3.
A. What is the probability that the last ball, drawn from box 3 is white?
B. What is the probability that the last ball drawn is black ball?
Answer by ikleyn(52772)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are three boxes containing black and white balls.
Box 1 contain 4 white ball, 2 black ball,
Box 2 contain 3 white ball and 2 black, and
Box 3 contain 1 white ball and 2 black.
Draw a ball from box 1 and place it in box 2.
Then draw a ball from box 2 and place it in box 3.
Finally draw a ball from box 3.
A. What is the probability that the last ball, drawn from box 3 is white?
B. What is the probability that the last ball drawn is black ball?
~~~~~~~~~~~~~~~~~~
Consider 1-st draw of the ball from Box1 to Box2.
With the probability 4/6 you move the white ball, and with probability 2/6 you move the black box.
So, after 1-st draw
a) with probability 4/6 we will have (4W,2B) in Box2, and
b) with probability 2/6 we will have ((3W,3B) there.
Now we consider 2-nd draw of the ball from Box2 to Box3.
We consider case a) first. It creates two sub-cases:
c) with probability 4/6 we move white ball and then we have then (2W,2B) in Box3;
d) with probability 2/6 we move black ball and then we have then (1W,3B) in Box3;
Next consider case b). It creates two sub-cases:
e) with probability 3/6 we move white ball and then we have then (2W,2B) in Box3;
f) with probability 3/6 we move black ball and then we have then (1W,3B) in Box3.
Now we analyse each and every of these chains of moves from B1 to B2 and then from B2 to B3 with their probabilities
to get what we will have at the end of each chain in Box 3.
The chain a) --> c) gives (2W,2B) in Box3 with probability 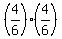 = = 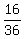 ; (1)
The chain a) --> d) gives (1W,3B) in Box3 with probability ; (1)
The chain a) --> d) gives (1W,3B) in Box3 with probability 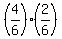 = = 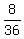 ; (2)
The chain b) --> e) gives (2W,2B) in Box3 with probability ; (2)
The chain b) --> e) gives (2W,2B) in Box3 with probability  = =  ; (3)
The chain b) --> f) gives (1W,3B) in Box3 with probability ; (3)
The chain b) --> f) gives (1W,3B) in Box3 with probability  = =  . (4)
Now the probability to get white ball from B3 is
P = . (4)
Now the probability to get white ball from B3 is
P = 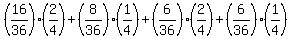 .
In this formula, the first factor in each addend is (1),(2),(3),(4); the second factor comes from the content of Box3.
Finally, P = .
In this formula, the first factor in each addend is (1),(2),(3),(4); the second factor comes from the content of Box3.
Finally, P = 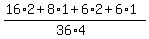 = = 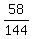 = = 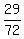 .
It is the ANSWER to question (A) of the problem. .
It is the ANSWER to question (A) of the problem.
-----------
So, part (A) is completed.
Part (B) is totally similar. I leave it as a useful exercise to you to check your understanding.
In any case, you just have this TEMPLATE in front of you.
|
|
|