SOLUTION: Find all solutions of each equation in the interval [0,2π) cos(x) + cos (3x) = 0

Algebra ->  Trigonometry-basics -> SOLUTION: Find all solutions of each equation in the interval [0,2π) cos(x) + cos (3x) = 0      Log On


   

Question 1155029: Find all solutions of each equation in the interval [0,2π)
cos(x) + cos (3x) = 0
Answer by ikleyn(52814) About Me  (Show Source):
You can put this solution on YOUR website!
.

The general statement is 


    If cos(a) + cos(b) = 0, then


        EITHER  a + b = pi + 2k%2Api

        OR      a - b = pi + 2k%2Api.


If apply it to  x  and  3x,  then


    EITHER  x + 3x = pi + 2k%2Api

    OR      |x - 3x| = pi + 2k%2Api.


First case gives

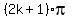    4x = %282k%2B1%29%2Api;  hence,  x = pi%2F4,  or  x = 3pi%2F4,  or  x = 5pi%2F4,  or  x = 7pi%2F4.


Second case gives

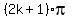   2x = %282k%2B1%29%2Api;  hence,  x = pi%2F2,  or  x = 3pi%2F2.


These 6 listed values are the full set of solutions to the given equation in given interval.

Solved.


Another approach is possible. 

Use the general formula


    cos(a) + cos(b) = 2%2Acos%28%28a%2Bb%29%2F2%29%2Acos%28%28a-b%29%2F2%29.


When you apply it with  x  and  3x, you get


    cos(x) + cos(3x) = 2*cos(2x)*cos(x) = 0,


which leads you to the SAME answer.

Solved.