SOLUTION: a. Find a polynomial of minimum degree such that when divided by x+2 has a remainder of -1 and when divided by x-1 has a remainder of 3. b. Find a polynomial of degree 3 such that

It is clear that the polynomial can not be linear (of the degree 1).


So, I will find such a polynomial of the degree 2 (quadratic).


Let f(x) = x^2 + bx + c be such a polynomial.


According to the Remainder theorem, the imposed conditions are equivalent to 

    f(-2) = -1  and  f(1) = 3,   or


    (-2)^2 - 2b + c = -1      (1)

    1^2    +  b + c =  3      (2)


Equations (1) and (2) are equivalent to


           - 2b + c = -5      (3)

              b + c =  2      (4)


From equation (3), subtract equation (4). You will get

            -3b     = -7;   hence,  b = .


Then from (4),  c = 2 - b = 2 -  = .


So, the polynomial is  f(x) = 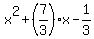 .    ANSWER


CHECK.  f(-2) = (-2)^2+(7/3)*(-2) - 1/3 = 4 - 14/3 - 1/3 = -1;

        f(1) = 1^2 + 7/3 - 1/3 = 1 + 2 = 3.    ! Correct !