SOLUTION: The sides of a square are parallel to the coordinate axes. Its vertices lie on the circle of radius 5 whose center is at the origin. Find coordinates for the four vertices of this

Let the coordinates of the four vertices be (-x,x), (-x,-x), (x,-x), and (x,x). 



Draw a radius (in green) from the origin (0,0) to a corner of the 
square. That makes an isosceles right triangle with hypotenuse
the green line, which is 5, since it is a radius of the circle.
Let the legs of the isosceles right triangle be x each.
We apply the Pythagorean theorem to the isosceles right triangle:



So the coordinates of the vertices are:

,,,

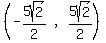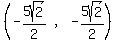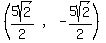Edwin