|
Question 1154714: Howard and Edward, working together, can complete a job in 12 hours. Edward requires 18 hours to do this job alone. Howard and Edward start the job. After they worked for 4 hours, Howard left the job. How many hours will Edward require to finish the job working alone?
Found 3 solutions by mananth, greenestamps, MathTherapy:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!
Howard and Edward, working together, can complete a job in 12 hours. Edward requires 18 hours to do this job alone. Howard and Edward start the job. After they worked for 4 hours, Howard left the job. How many hours will Edward require to finish the job working alone?
Edward requires 18 hours to do this job alone.
He does 1/18 of job in 1 hour
Howard and Edward start the job they worked for 4 hours,
They can complete the job in 12 hours
So they can do 1/12 of the job in 1 hour
they worked for 4 hours
so they completed 4/12 of the job = 1/3 of the job
balance job = 1-1/3 = 2/3 of the job
Edward does 1/18 of job in 1 hour
for 1/3 of the job he will take (1/3)/(1/18) hours
(1/3) *18
6 hours
Edward will take 6 hours to complete the job
Answer by greenestamps(13215)  (Show Source):
You can put this solution on YOUR website!
They take 12 hours to do the job together.
In the beginning, they work together for 4 hours. The fraction of the job that gets done is 4/12 = 1/3; 2/3 of the job remains.
Edward takes 18 hours to do the job alone. To do the 2/3 of the job that remains alone, the required amount of time is 2/3 of 18 hours, or 12 hours.
Answer by MathTherapy(10557)  (Show Source):
You can put this solution on YOUR website! Howard and Edward, working together, can complete a job in 12 hours. Edward requires 18 hours to do this job alone. Howard and Edward start the job. After they worked for 4 hours, Howard left the job. How many hours will Edward require to finish the job working alone?
6 hours is WRONG!!
If both can do the job in 12 hours, then in 4 hours, they will have done: 
With  of work completed by both, in 4 hours, 
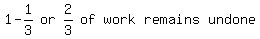
With Edward taking 18 hours to do entire job alone, and doing  of job in 1 hour, time (T) taken by Edward to complete remaining  of job is: 
T, or time taken by Edward to complete remaining of job = 
|
|
|
| |
