|
Question 1154678: How do you find the area of a polygon ABCDE with vertices A(0,0), B(0,4), C(8,8), D(14,0), and E(9,-2)
Found 5 solutions by Alan3354, MathLover1, MathTherapy, ikleyn, greenestamps:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! How do you find the area of a polygon ABCDE with vertices A(0,0), B(0,4), C(8,8), D(14,0), and E(9,-2)
----------
There's more than one way.
The simplest, IMO, is this:
-----
A B C D E A
0 0 8 14 9 0
0 4 8 0 -2 0
----------------
Add the diagonal products starting at the upper left.
0*4 + 0*8 + 8*0 + 14*-2 + 9*0 = 0+0+0-28+0 = -28
---
Add the diagonal products starting at the lower left.
0*0 + 4*8 +8*14 + 0*9 + -2*0 = 0+32+112+0+0 = 144
-----------
The difference is 172
The area is 1/2 that = 86 sq units.
============
The points have to be in order around the figure.
I think it works for all polygons, not just convex.
========================
PS Graphing it is a good idea, to ascertain that the points are in order around the polygon.
Answer by MathLover1(20850)  (Show Source):
You can put this solution on YOUR website!
first graph it
 ( ,)
 (, )
 ( ,)
 ( ,)
 ( , )
the length of the side 
the length of the side  :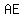
=>
the length of the side  :
=>
the length of the side  :
=>
the length of the side  :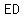
=>
The area of any irregular quadrilateral can be calculated by dividing it into triangles.
Heron's Formula for the area of a triangle(Hero's Formula)
A method for calculating the area of a triangle when you know the lengths of all three sides.
Let  , , be the lengths of the sides of a triangle.
The area is given by:
 where is half the perimeter, or 
divide in triangles:
you have triangles ABC, ACD, and AED
the area of triangles  :
sides:
find side 
 =>the area of triangle
find the area of triangle 
 =>the area of triangle
find the area of triangle  :
 =>the area of triangle
the area of triangles 
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! How do you find the area of a polygon ABCDE with vertices A(0,0), B(0,4), C(8,8), D(14,0), and E(9,-2)
I got the same thing Tutor @ALAN got:  . I also used the same method!
If you want to TORTURE yourself, then follow the other person's solution, which by the way should be 86 sq units, NOTHING more, NOTHING LESS.
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
By the way, there is another elementary method calculating the area of a polygon.
Place it into a rectangle with vertical and horizontal sides.
Make this rectangle as small as possible, i.e. get the polygon "inscribed" into the rectangle.
Calculate the area of the rectangle (which is easy).
Then subtract the areas of all excessive triangles, by "cutting" them.
It is very easy, too.
Doing in this way, you will get the answer.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Breaking the figure into three triangles and finding the area of each is an astonishingly bad (and tedious!) way to try to get the answer...!
The matrix method for solving the problem, used by a couple of the other tutors, is clearly the easiest way to get the answer. But the method suggested by another tutor of inscribing the given figure in a rectangle is also an easy method.
I will steal another tutor's figure and add to it to find the answer by this method.
The area of rectangle PQRS (dimensions 14x10) is 140.
The area of right triangle BPC (legs 4 and 8) is 16
The area of right triangle CQD (legs 6 and 8) is 24
The area of right triangle DRE (legs 2 and 5) is 5
The area of right triangle ESA (legs 2 and 9) is 9
The area of polygon ABCDE is 140-(16+24+5+9) 140-54 = 86.
|
|
|
| |
