SOLUTION: Hi A person covers 2/3 of his journey at his usual speed and the remaining distance at 3/4 of the usual speed and takes 30min more than the usual time. If total distance is 180

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Hi A person covers 2/3 of his journey at his usual speed and the remaining distance at 3/4 of the usual speed and takes 30min more than the usual time. If total distance is 180      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1154666: Hi
A person covers 2/3 of his journey at his usual speed and the remaining distance at 3/4 of the usual speed and takes 30min more than the usual time. If total distance is 180km what is the usual speed.
Thanks
Found 3 solutions by mananth, math_helper, ikleyn:
Answer by mananth(16946) About Me  (Show Source):
You can put this solution on YOUR website!

A person covers 2/3 of his journey at his usual speed and the remaining distance at 3/4 of the usual speed and takes 30min more than the usual time. If total distance is 180km what is the usual speed.
2/3 * 180 =120

let the usual speed be x km/h
distance 120 km
time = 120/x First part
distance = 60 km
speed = 3x/4
Time taken = 60/(3x/4)
=240/3x
=80/x II part
120/x +80/x = 180/x + 1/2 ( 30 minutes =1/2)
200/x = 180/x +1/2
20/x = 1/2
x= 40 km/h






Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!


Make use of distance = rate * time:

d = r*t 



where we solve for t:

t = d/r  





Notation

S%5Bu%5D+ = usual speed

t%5Bu%5D+ = usual time



  (1) (time in hours)



So far, one equation with two unknowns.  We find the 2nd equation by noting equation for the usual speed:

+180%2FS%5Bu%5D+=+t%5Bu%5D+   (2)



From here, substitute the LHS of (2) into the RHS of (1) and solve to get:

+highlight%28S%5Bu%5D+=+40%28km%2Fhr%29%29+





Check:

180km/(40km/hr) = 4.5hrs (the usual time)



(2/3)(180)/40 + (1/3)(180)/((3/4)40) = 3hrs + 2hrs = 5hrs  (1/2hr longer than the usual time, so this is ok)

Answer by ikleyn(52835) About Me  (Show Source):
You can put this solution on YOUR website!
.

            I'd like to contribute my  2  cents to this problem's solution. 


It is clear that we can exclude the first 2/3 of the journey from the consideration,
since at this part there is no delay comparing with the standard schedule.


The difference arises on the remained 1/3 distance, which is 60 miles.


For this part of 60 miles, we have a regular time  60%2Fx, where x is the regular speed.


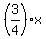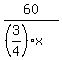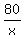With the speed of %283%2F4%29x, the spent time is  60%2F%28%283%2F4%29x%29 = 80%2Fx.


So, the delay equation is


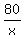    80%2Fx - 60%2Fx = 1%2F2   (which is half of an hour)


From the equation,  


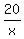    20%2Fx = 1%2F2;

hence,

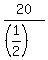    x = 20%2F%28%281%2F2%29%29 = 2*20 = 40 kilometers per hour.    ANSWER

Solved.

I hope that my setup is simpler and, therefore, more attractive.