Question 115458: Please help. Please.
Graph the following inequality. Please show how to create the dotted or dashed line,
2x+3y>6
Thanks
JMS
Found 2 solutions by aka042, clpro1974:
Answer by aka042(26)   (Show Source):
You can put this solution on YOUR website! Let's first re-write the inequality to have y by itself on the left side.
To do this, we first need to subtract 2x from both sides. This gives us: 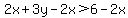 , which simplifies to  .
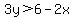Next, we need to divide through by three: 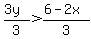 , which simplifies to  .
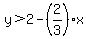As a rule, where E is some expression involving x and a constant:
You draw a dotted line if you have y > E or y < E
You draw a solid line if you have  or 
We are going to draw a dotted line.
To draw the line, we just replace the > with =. Therefore, we are graphing the line  . This line intercepts the y axis at 2, and slopes downward (2/3). Draw a point at (0,2), your y-intercept. Now draw another point at (3,0). We choose x=3 for simplicity's sake (2/3 * 3 = 2, an integer). You can really choose any x value you'd like though.
Draw a dotted line connecting these two points.
Now for the last step: we are really graphing 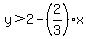 , so we are looking for all y values GREATER than  . Therefore, shade the region ABOVE the dotted line you have drawn.
We have now successfully graphed the inequality.
Answer by clpro1974(1) (Show Source):
You can put this solution on YOUR website! Hello,
First, you want to get your equation in y=mx+b (slope intercept form)
m=is always your slope, b=is always your y-intercept.
2x+3y>6 1st get y by itself.
-2x -2x subtract 2x from both sides
---------
3y>-2x+6 Almost there, now we will divide 3 under all terms to get y alone.
y>-2x/3=2
****Note pay attention to dividing, if you divide by a negative number your >will change sign
direction to < .
Now you are in slope intercept form y=mx+b
draw out your graph put a dot at point +2 on the y-axis (this is "b" in y=mx+b formula)
-2
-- now look at the slope
3
count down two places on your graph then right three places.
You should have dots at (0,2) to start then (3,0) and (-3,4)
< and >are always dotted lines, ≥ and ≤ are solid lines.
Hope this is what your looking for & helps:)
|
|
|
