SOLUTION: i need help with this one thank you 3x^2+2y^2-6x+12y=0

Algebra ->  Graphs -> SOLUTION: i need help with this one thank you 3x^2+2y^2-6x+12y=0       Log On


   

Question 115453This question is from textbook Algebra and Trigonometry
: i need help with this one thank you
3x^2+2y^2-6x+12y=0
This question is from textbook Algebra and Trigonometry

Answer by aka042(26) About Me  (Show Source):
You can put this solution on YOUR website!
Because your equation contains both x^2 and y^2 terms, we can conclude that we are going to be graphing some sort of ellipse.
In general, ellipses are always given in the following form: %28%28x-h%29%5E2%2Fa%5E2%29+%2B+%28%28y-k%29%5E2%2Fb%5E2%29+=+1. h and k indicate the center of the ellipse, while a and b indicate the two points of greatest distance from your center.
Let's re-arrange your equation to put the x and y terms together: 3x%5E2+-+6x+%2B+2y%5E2+%2B12y+=+0. Now let's remove the coefficients from x^2 and y^2:
3%28x%5E2+-+2x%29+%2B+2%28y%5E2+%2B6y%29+=+0.
We are now going to use a method called "complete the square" to arrive at the desired form of your equation.
To complete the square, let's first look at your x terms: 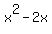x%5E2+-+2x. Completing the square tells us to take half of whatever precedes x (its coefficient), and then square that. Half of -2 is -1, and -1 squared = 1.
Similarly, for your y terms: y%5E2+%2B+6y, we will take half of 6 which is 3, and then square that to arrive at 9. Now we add these two numbers to both sides to arrive at the following equation:
3%28x%5E2+-+2x+%2B+1%29+%2B+2%28y%5E2+%2B+6y+%2B+9%29+=+0+%2B+3%281%29+%2B+2%289%29+=+21.
We now have two easily factorable expressions of x and y:
3%28x-1%29%5E2+%2B+2%28y%2B3%29%5E2+=+21. Finally, we have to divide both sides through by 21 to arrive at the general formula for an ellipse (notice that the formula given at the top of this solution requires the right side to = 1).
Therefore our final equation is: %281%2F7%29%2A%28x-1%29%5E2+%2B+%282%2F21%29%2A%28y%2B3%29%5E2+=+1. Let's rewrite this as: %28%28x-1%29%5E2%2F%287%29%29+%2B+%28%28y%2B3%29%5E2%2F%2821%2F2%29%29+=+1+.
Therefore, h= 1 and k=-3, so your ellipse is centered at (1, -3). Draw a point there on your graph.
a%5E2+=+7, which means a+=+sqrt%287%29 or a+=+-sqrt%287%29. The square root of 7 is about 2.65, so move a little more than 2.5 to the right along the line y=-3 from your center and draw another point there. Do the same but this time moving to the left a little more than 2.5 spaces from your center.
b%5E2+=+%2821%2F2%29, which means b=sqrt%2821%2F2%29 or b+=+-sqrt%2821%2F2%29. The square root of (21/2) is about 3.24, so now move up a little more than three spaces from your center along the x = -1 line and draw a point there. Do the same, this time moving a little more than three spaces down from your center.
Finally, connect the points using curved lines and you have your ellipse!