SOLUTION: root of x raised to the power log x equals 100

Algebra ->  Exponential-and-logarithmic-functions -> SOLUTION: root of x raised to the power log x equals 100       Log On


   

Question 1154501: root of x raised to the power log x equals 100
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

The original equation is

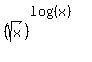    %28sqrt%28x%29%29%5E%28log%28%28x%29%29%29 = 100.


The domain is  { x | x > 0 }.


The equation is equivalent to

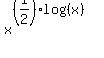    x%5E%28%281%2F2%29%2Alog%28%28x%29%29%29 = 100.


Square both sides.   You will get

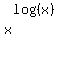    x%5E%28log%28%28x%29%29%29 = 10000.


Take logarithm base 10 from both sides.  You will get

    log(x) * log(x) = log(10000),   or

    (log(x))^2 = log(10000),  or

    (log(x))^2 = 4.


Take square root from both sides.  You will get

    log(x) = +/- 2.


So we have two solutions

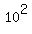    1)  log(x) = 2,  x = 10%5E2 = 100,   and


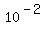    2)  log((x) = -2,  x = 10%5E%28-2%29 = 1%2F100.


ANSWER.  The original equation has two solutions,  x = 100  and  x = 1%2F100.

Solved.