SOLUTION: Four raised to the power x plus 6 to the power x equals 9 to the power x

The given exponential equation


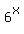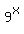     +  =              (1)


is equivalent to


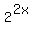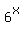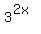     +  = ,   or


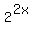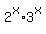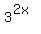     +  = .          (2) 


Introduce new variables  u = 2^x,  v = 3^x.  Then equation (2) takes the form

    u^2 + u*v = .


Divide both sides by u^2.  You will get

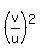     -  - 1 = 0                (3)


Let z = .   Then equation (3) takes the form

    z^2 - z - 1 = 0.


Solve this quadratic equation using the quadratic formula


     =  = .


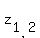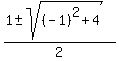The roots are  

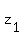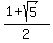     = ,   and

     = .


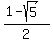Thus, we should consider two cases.


(a)   = .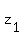


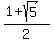     It means   =  = .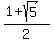


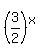     Next, take any logarithm, log base 10, or natural logarithm "ln"  from both sides to continue


        = ,

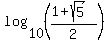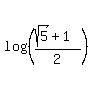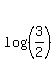        x =  /  =  = 1.1868  (approximately).


    Thus this case is completed.



(b)   = - 


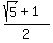     It means  -  =  = .

     
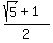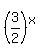     The left side is negative, while the right side is positive.


     So, this case has no solutions.
     

ANSWER.  The original equation has only one root  x = 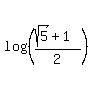 /  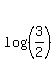=  = 1.1868  (approximately).