Question 1154460: A ball is thrown in the air from the top of a building. Its height, in meters above ground, as a function of time, in seconds, is given by
h(t) = −4.9t2 + 16t + 14.
How long does it take to reach maximum height? (Round your answer to three decimal places.)
Found 2 solutions by josmiceli, ikleyn:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by ikleyn(52847)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It is about finding the value of time "t", which maximize the given quadratic function.
For any quadratic function y(x) = ax^2 + bx + c with the negative leading coefficient "a",
the value of the variable x, which provides the maximum to y(x), is x=  .
In your case, a = -4.9, b = 16, so the value of time "t" is
t = .
In your case, a = -4.9, b = 16, so the value of time "t" is
t = 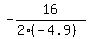 = = 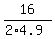 = 1.633 seconds. ANSWER = 1.633 seconds. ANSWER
Solved, answered, calculated, explained and completed.
-----------------------------
My other lessons in this site on finding the maximum/minimum of a quadratic function are
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|