|
Question 115443: Please help, I have to turn my homework in today and I am totaly confused witht his question.
Find the horizontal and vertical asymptote of the following. Type "none" if the function does not have an asymptote.
f(x)= 2x-3/x^2+2
Horizontal:
Vertical:
Thank you in advance for your help.
Found 2 solutions by solver91311, ganesh:
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Rational functions have a vertical asymptote where the denominator goes to zero. But the denominator of this function has no real zeros because there is no real number x such that  . Therefore there are no vertical asymptotes. . Therefore there are no vertical asymptotes.
To investigate the possibility of a horizontal asymptote, examine the function in terms of what happens when x gets very large. We can see that the denominator is going to get larger much faster than the numerator in this case, so the function is going to tend to zero. Since  is a zero of the function, the function will be positive on the interval ( is a zero of the function, the function will be positive on the interval ( , , ) and will be negative on the interval ( ) and will be negative on the interval ( , , ) )
So we know that as x decreases without bound, the function will tend to zero, but be negative.
What I have given you is an intuitive look at the problem. To actually determine and prove the horizontal asymptote to this function you need to use the concept of a limit from Calculus. In this case, we need to use the general rule that:
If g(x) and h(x) are functions such that the degree of g is smaller than the degree of h, then  . Since the degree of . Since the degree of 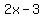 is 1 and the degree of is 1 and the degree of 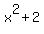 is 2, we can say that is 2, we can say that  . This is sufficient to establish the horizontal asymptote at . This is sufficient to establish the horizontal asymptote at  . We also know that this is the only horizontal asymptote because rational functions have at most 1 horizonal asymptote. . We also know that this is the only horizontal asymptote because rational functions have at most 1 horizonal asymptote.

Answer by ganesh(20)   (Show Source): (Show Source):
You can put this solution on YOUR website! General Rule:
To find the vertical asymptote:
Find the solutions for the denominator function. That solutions are the vertical asymptote.
In our problem, denominator is x^2 + 2.
Consider the equation x^2 + 2 = 0
We get x^2 = -2
x = + or - sqrt{-2}
It has no real solution. ( since we cannot find a real number as the square root of -2)
So, the rational function does not have any vertical asymtote.
To find the horizontal asymtote:
Find limit x tending to infinity f(x).
The limit value is the horizontal asymptote.
In our problem, Limit x tending to infinity f(x) = 0.
So, f(x) = y = 0 is the horizontal asymptote.
Finally,
Horizontal: y = 0
Vertical : None.
|
|
|
| |