Question 1154211: You collect four shells from the beach. You know that there are only three types of shells on the beach, and these shells occur in equal amounts. How many different events are possible?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The space of events consists of all 4-digit numbers written with digits 1, 2 and 3,
where each digit represents one of the three types of shells.
Repeating is allowed for these digits.
The number of all elements (of all 3-digit numbers of this kind) is  = 81, because in each of the 4 positions any of 3 digits may occur. = 81, because in each of the 4 positions any of 3 digits may occur.
The probability for each individual element of the space of events is  . .
----------------
The solution above works when the order of shells in the collection is important (does matter).
We may consider other extreme case when the order of shells in the collection DOES NOT MATTER (is not important).
Then the set of events is the set of all different solutions to equation
 + +  + +  = 4 (1) = 4 (1)
in integer non-negative numbers.
Here each of the numbers  , ,  , ,  represents the MULTIPLICITY of the shell of the type "i" in the collection, i = 1, 2, 3. represents the MULTIPLICITY of the shell of the type "i" in the collection, i = 1, 2, 3.
There is the formula for the number of solution to equation (1) under given restriction
the number of solution = 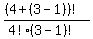 = = 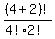 = = 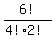 = = 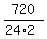 = = 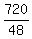 = 15. = 15.
Thus in this case the space of events has 15 elements with equal probability of  each. each.
The method calculating the number of solutions to equation (1) is called the "Stars and Bars method".
You can read about it in the lesson
- Stars and bars method for Combinatorics problems
in this site, Problem 2.
--------------------
Notice after reading the post by @greenestamps.
The formula in the post by @greenestamps is correct, and his answer is correct, too.
The formula in my original post was incorrect.
Many thanks to greenestamps for noticing it (!)
After detecting my error, I fixed my formula and re-calculated the answer.
Now you see the edited version in my post, which agrees with the solution by @greenestamps.
Again, many thanks to @greenestamps (!)
It is nice to have so attentive, accurate and knowledgeable colleague !
/\/\/\/\/\/\/\/
-------------
Comment from student: Hi ikleyn, Thank you for your urgent response to my question.
However, I am a bit confused with your answer. The reason is because, I looked at this task in the context of probability.
If so, can we have a probability greater than 1?
-------------
My response.
Hello, I got this comment from a visitor. But since it came with no reference to the problem,
I don't know to WHICH PROBLEM it relates.
If it relates to THIS problem, then where do you see the word "probability" in your post?
In the future, if you want to have a DIALOG, then PLEASE REFER to the ID number of the problem, which is 1154211 in this case.
If the comment and the question do not relate to this problem, then ignore/disregard my post.
Have a nice day (!)
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If only the numbers of shells of the different types counts, there are 15 combinations:
(4,0,0), (0,4,0), (0,0,4)
(3,1,0), (3,0,1), (1,3,0), (0,3,1), (1,0,3), (0,1,3)
(2,2,0), (2,0,2), (0,2,2)
(2,1,1), (1,2,1), (1,1,2)
This is a common type of problem, adding a certain number of whole numbers to get a certain total. This kind of problem can be solved using "stars and bars".
Imagine picking up the shells and putting them in one of three bins to separate them by the type of shell.
Now model that by imagining the four shells arranged in a row, and you place two dividers between the shells to represent dividing them into the three types. Note that only (n-1) dividers are needed to separate the items into n types.
Represent the shells with stars and the dividers with bars. We have a string of six items -- the four shells and the two dividers.
Each different arrangement of the six items represents a different distribution of the four shells among the three types. For example,
**|*|* represents two shells of the first type and one each of the other two types;
|***|* represents three shells of the second type and one of the third.
By a well-known counting principle, the number of different arrangements of those four stars and two bars is

In general, if there are n items to be divided into k groups, there are n stars and (k-1) bars, and the number of ways of distributing the items is
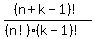
Note a similar kind of problem requires that the total be composed of POSITIVE integers (i.e., there must be at least one item of each type). In that case, simply take one item an put it in each bin; then use stars and bars to distribute the remaining (n-k) items.
For this problem, we start with one of each of the three types of shells, leaving us with one more shell to "distribute" among the three types. Obviously there are three ways to do that, as can be seen in the list of possible distributions at the beginning of this response.
Using stars and bars, that is represented by the possible arrangements of the symbols
*||
There are obviously three different arrangements; if you wanted to use the formula to get that total, it would look like

|
|
|