Question 1154178: ‚ÄãHere's my‚Äã dilemma, I can accept a ‚Äã$1000 bill or play a game ten times. For each
roll of the single‚Äã die, I win ‚Äã$600 for rolling 1 or‚Äã 2; I win ‚Äã$400 for rolling‚Äã 3;
and I lose ‚Äã$100 for rolling‚Äã 4, 5, or 6. Based on the expected‚Äã value, Should I
accept the ‚Äã$1000 bill? What is the expected value in dollars?
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website! ‚ÄãHere's my‚Äã dilemma, I can accept a ‚Äã$1000 bill or play a game ten times. For each
roll of the single‚Äã die, I win ‚Äã$600 for rolling 1 or‚Äã 2; I win ‚Äã$400 for rolling‚Äã 3;
and I lose ‚Äã$100 for rolling‚Äã 4, 5, or 6. Based on the expected‚Äã value, Should I
accept the ‚Äã$1000 bill? What is the expected value in dollars?
Winnings Probability Expectation
or of winning
losses or losing
+$600 2/6 600(2/6) = +$200
+$400 1/6 -400(1/6) = -$ 66.67
-$100 3/6 100(3/6) = +$ 50.00
Total expectation = +$183.33
One might think it wiser to accept the $1000 bill, which would be wise
if it were are genuine $1000-bill. However I suspect this might be a trick
question and that it would be wiser to play the game since you would stand
a good chance of winning. A $1000-bill is sure to be counterfeit because no
$1000 bills are in circulation. J
Edwin
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Since the solution by Edwin is INCORRECT (unfortunately),
I came to provide the correct solution.
The probability to win $600 is 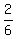 ;
the probability to win $400 is ;
the probability to win $400 is  ;
the probability to lose $100 is ;
the probability to lose $100 is  .
Mathematical expectation is .
Mathematical expectation is 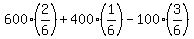 = = 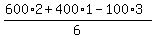 = = 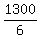 = 216.6666666.....
It means that in EACH game you may expect to win 216.67 dollars as your winning prize.
More precisely, it means, that if you play this game many times, your averaged winning sum
will be about 216.67 dollars.
In turn, it means that in 10 games you may expect to win 10 times this value, i.e $2,166.67.
Again, in 10 games you may accumulate 2,166.67 dollars as your winning prize, in total.
In wording form TWO THOUSAND one hundred sixty six dollars and 67 cents.
Now turn on your mind and compare it with $1000. = 216.6666666.....
It means that in EACH game you may expect to win 216.67 dollars as your winning prize.
More precisely, it means, that if you play this game many times, your averaged winning sum
will be about 216.67 dollars.
In turn, it means that in 10 games you may expect to win 10 times this value, i.e $2,166.67.
Again, in 10 games you may accumulate 2,166.67 dollars as your winning prize, in total.
In wording form TWO THOUSAND one hundred sixty six dollars and 67 cents.
Now turn on your mind and compare it with $1000.
Note, that it is not my advise for you to follow it in real life (and do not consider it as my advise, please (!) )
I am not responsible for the consequences (!) (!) (!)
It is the solution of the given Math problem ONLY.
|
|
|