Question 1154150: We select three balls randomly (one after another) of a box contains 1 white, 2 yellow and 3 blue balls. If all balls have the same chance of selecting, then:
a) What is the probability that the selected balls have the same color ?
b) What is the probability that no white balls have been selected ?
c) What is the probability that all [BOTH] yellow balls are selected ?
Found 3 solutions by ikleyn, greenestamps, Edwin McCravy:
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In this problem, the probability is the ratio/fraction, whose denominator is the same for all 3 parts, a), b) and c).
This denominator is 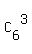 = = 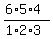 = 20, and it represents the number of triples that can be formed from 6 = 1+2+3 balls.
The numerator is different for each part. It is the number of favorable triples in each case.
(a) In this case, there is only one favorable triple, consisting of 3 blue balls.
Thus the probability in this case is P = = 20, and it represents the number of triples that can be formed from 6 = 1+2+3 balls.
The numerator is different for each part. It is the number of favorable triples in each case.
(a) In this case, there is only one favorable triple, consisting of 3 blue balls.
Thus the probability in this case is P =  = 0.05.
(b) In this case, favorable triples can be formed from 5 = 2+3 yellow and blue balls.
The number of favorable triples is, therefore, = 0.05.
(b) In this case, favorable triples can be formed from 5 = 2+3 yellow and blue balls.
The number of favorable triples is, therefore, 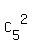 = 10.
Thus the probability in this case is P = = 10.
Thus the probability in this case is P = 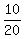 = =  = 0.5.
(c) This time the triples contain 2 yellow balls, and we can add EITHER 1 white or any one of 3 blue balls.
Hence, the number of different favorable triples in this case is 1+3 = 4.
Therefore, the probability is P = = 0.5.
(c) This time the triples contain 2 yellow balls, and we can add EITHER 1 white or any one of 3 blue balls.
Hence, the number of different favorable triples in this case is 1+3 = 4.
Therefore, the probability is P = 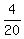 = =  = 0.2. = 0.2.
Solved. // All questions are answered.
Answer by greenestamps(13198)   (Show Source): (Show Source):
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
With this kind of problem, you must specify whether it's "SELECTING WITH
REPLACEMENT" or "SELECTING WITHOUT REPLACEMENT". You didn't specify I will have
to do it both ways.
If it's WITHOUT replacing, then we will think of reaching in one time and
drawing out 3, so we will use combinations, for you don't care which of the
three balls is drawn first, second or third when you just reach in and get a
handful of 3 balls.
a) What is the probability that the selected balls have the same color?
WITHOUT REPLACEMENT:
There is only 1 'successful' way, which is to choose all 3 blue balls.
The number of ways to choose ANY three balls is
6 balls CHOOSE 3 = 6C3 = 20
So the probability is 1 way out of 20 or 1/20 or 0.05 or 5% of the time.
--------------------------------------------
a) What is the probability that the selected balls have the same color ?
WITH REPLACEMENT:
Case 1: three whites.
The first drawn is white, we do that 1/6 of the time.
The second drawn is white, we also do that 1/6 of the time.
The third drawn is white, we also do that 1/6 of the time.
So (1/6)³ = 1/216 of the time we'll draw 3 whites.
Case 2: three yellows.
The first drawn is yellow, we do that 2/6 or 1/3 of the time.
The second drawn is yellow, we also do that 2/6 or 1/3 of the time.
The third drawn is yellow, we also do that 2/6 or 1/3 of the time.
So (1/3)³ = 1/27 of the time we'll draw 3 yellows.
Case 3: three blues.
The first drawn is blue, we do that 3/6 or 1/2 of the time.
The second drawn is blue, we do that 3/6 or 1/2 of the time.
The third drawn is blue, we do that 3/6 or 1/2 of the time.
So (1/2)³ = 1/8 of the time we'll draw 3 blues.
So the total probability for all three cases is
 ---------------------------------------------------------------------
b) What is the probability that no white balls have been selected?
WITHOUT REPLACING:
That means we draw 3 balls from the 5 non-white balls.
That's 5 non-white balls CHOOSE 3 or 5C3 = 10 ways.
10 ways out of 20 is 10/20 with reduces to 1/2
------------------------------------------------
WITH REPLACING.
c) What is the probability that all [BOTH] yellow balls are selected ?
We pick the two yellows 1 way.
We pick the 1 non-yellow to go with the two yellows in 4 ways.
So there are 1∙4=4 ways to have a combination of 3 including both yellows.
That's 4 ways out of 20 or 4/20 which reduces to 1/5.
Edwin
---------------------------------------------------------------------
b) What is the probability that no white balls have been selected?
WITHOUT REPLACING:
That means we draw 3 balls from the 5 non-white balls.
That's 5 non-white balls CHOOSE 3 or 5C3 = 10 ways.
10 ways out of 20 is 10/20 with reduces to 1/2
------------------------------------------------
WITH REPLACING.
c) What is the probability that all [BOTH] yellow balls are selected ?
We pick the two yellows 1 way.
We pick the 1 non-yellow to go with the two yellows in 4 ways.
So there are 1∙4=4 ways to have a combination of 3 including both yellows.
That's 4 ways out of 20 or 4/20 which reduces to 1/5.
Edwin
|
|
|