SOLUTION: Jerry can complete a sales route​ by himself in 8 hours. Working with an associate, he can complete a sales route in 5 hours. How long would it take his associate to do it workin

Algebra ->  Rational-functions -> SOLUTION: Jerry can complete a sales route​ by himself in 8 hours. Working with an associate, he can complete a sales route in 5 hours. How long would it take his associate to do it workin      Log On


   

Question 1154132: Jerry can complete a sales route​ by himself in 8 hours. Working with an associate, he can complete a sales route in 5 hours. How long would it take his associate to do it working alone?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
Jerry averages 1%2F8 of the route every hour
associate averages 1%2Fa
working with an associate: averages 1%2F5
1%2F8+%2B+1%2Fa+=+1%2F5
1%2Fa+=+1%2F5-1%2F8+
1%2Fa+=+8%2F40-5%2F40
1%2Fa+=+3%2F40
40=3a
a=40%2F3
a=+13%261%2F3h or 13h20min

Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.

            This problem  (and many other similar joint work problems)  can be solved by different ways.

            The other tutor showed you the solutions using equation.

            But the problem can be solved without using equations,  by manipulating fractions only. 


When both do the job together, they make  1%2F5  of the job per hour.


When Jerry makes it alone, he completes  1%2F8  of the job per hour.


Hence, the associate makes  1%2F5 - 1%2F8  of the job per hour.


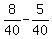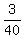    1%2F5 - 1%2F8 = 8%2F40+-+5%2F40 = 3%2F40.


It means that the associate will complete the job in  40%2F3 hours = 131%2F3 hours = 13 hours and 20 minutes.

Solved.

In this way,  you do not need solve equation.  You only manipulate fractions.

I believe,  you will feel yourself much more confident,  when you know this approach.

This approach has two  (at least,  two)  benefits comparing with using equations.

First,  even young students can solve such problems,  who ddn't study equations yet,  but know fractions.

The second benefit is that they will learn and will understand the notion  (the conception)  of  "rate of work",
which is,  usually,  goes out  (goes away,  disappears),  when they are touched to use equations only.

----------------

It is a standard and typical joint work problem.

There is a wide variety of similar solved joint-work problems with detailed explanations in this site.  See the lessons
    - Using Fractions to solve word problems on joint work
    - Solving more complicated word problems on joint work
    - Selected joint-work word problems from the archive


Read them and get be trained in solving joint-work problems.

Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this textbook under the topic
"Rate of work and joint work problems"  of the section  "Word problems".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.