SOLUTION: Consider the following system of linear equations. 3x − 2y + z = 4 x + y − z = 2 x + z = 1 (i) Write the system in the form Ax = b. (ii) Use the determinant to show that A

Algebra ->  Linear-equations -> SOLUTION: Consider the following system of linear equations. 3x − 2y + z = 4 x + y − z = 2 x + z = 1 (i) Write the system in the form Ax = b. (ii) Use the determinant to show that A      Log On


   

Question 1153962: Consider the following system of linear equations.
3x − 2y + z = 4
x + y − z = 2
x + z = 1
(i) Write the system in the form Ax = b.
(ii) Use the determinant to show that A is invertible.
(iii) Find the inverse of A using the Gauss-Jordan elimination.
(iv) Find the inverse of A using the determinant and the adjoint of A, i.e.,
A
−1 =
1
det(A)
adj(A).
(v) Comment on your answers in part (iii) and (iv).
(vi) Solve the system using the inverse matrix found in part (iv).
Answer by Edwin McCravy(20063) About Me  (Show Source):
You can put this solution on YOUR website!


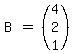matrix%281%2C3%2CB%2C%22%22=%22%22%2C%0D%0A%28matrix%283%2C1%2C4%2C2%2C1%29%29%29

We write the system it in the form AX = B,




Next we show that the determinant of the matrix A is not 0, which
tells us that the matrix A has an inverse A-1. We expand
the matrix across the bottom row since it contains a 0:




}}}

We find the inverse of A by the Gauss-Jordan method.
We augment A with the identity matrix:



Use row operations to get the identity on the left:
Swap the 1st and 3rd rows:



Multiply R1 by -1 and add to R2, restoring R1 after multiplying:



Multiply R1 by -3 and add to R3, restoring R1 after multiplying:



Multiply R2 by 2 and add to R3, restoring R2 after multiplying:



To avoid fractions till the last step, multiply R1 by 6



Add R3 to R1



Also to avoid fractions till the last step, multiply
R2 by -3



Add R3 to R2



Divide R1 through by 6,
Divide R2 through by -3
Divide R3 through by -6



So the inverse of A is the right half of the above,





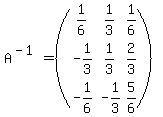Now find the adjoint of

%28matrix%283%2C3%2C3%2C-2%2C1%2C1%2C1%2C-1%2C1%2C0%2C1%29%29

First we find the matrix of signed minor determinants:



which is

%28matrix%283%2C3%2C1%2C-2%2C-1%2C2%2C2%2C-2%2C1%2C4%2C5%29%29

Then its transpose is the adjoint:

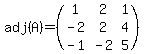adj%28A%29=%28matrix%283%2C3%2C1%2C2%2C1%2C-2%2C2%2C4%2C-1%2C-2%2C5%29%29

Then we substitute in the formula

matrix%281%2C3%2C%0D%0A%0D%0AA%5E%28-1%29%2C%22%22=%22%22%2Cadj%28A%29%2Fabs%28A%29%29

which says to divide every element of the adjoint matrix
by the determinant of A, which we have calculated to be 6.
So we get the same inverse:


----------------
Both methods are tedious and very time-consuming by hand. You are prone to make
a mistake.  Since we now have graphing calculators which can find inverses
easily, that's the way we should do them.
----------------

Next we left multiply both sides of this matrix equation:

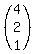%22%22=%22%22%28matrix%283%2C1%2C4%2C2%2C1%29%29

by the inverse matrix



and get this equation:

%22%22=%22%22

Now I will assume that you know how to multiply two matrices.  If
you don't know how, then post again asking how to.  When you
multiply the red matrices by the black matrices just to the right of
each red ones, you get this:

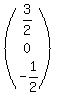%22%22=%22%22%28matrix%283%2C1%2C3%2F2%2C0%2C-1%2F2%29%29

Notice that when you multiply the inverse of a matrix by the matrix
of which it is the inverse you get the identity matrix, which has
1's on the diagonal and 0's elsewhere.

Now if you multiply the two matrices on the left and on the right
and you get:

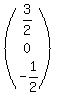%28matrix%283%2C1%2Cx%2Cy%2Cz%29%29%22%22=%22%22%28matrix%283%2C1%2C3%2F2%2C0%2C-1%2F2%29%29

and so x=3/2, y=0, and z=-1/2.

Edwin