Question 1153924: A manufacturing company makes two types of water skis, a trick ski and a slalom ski. The relevant manufacturing data are given in the table:
LABOR HRS
MAX LABOR HRS AVAILABLE PER DAY
DEPT Trick Ski Slalom Ski
Fabricating 8 6 264
Finishing 1 1 40
(A) If the profit on a trick ski is $40 and the profit on a slalom ski is $50, how many of each type of ski should be manufactured each day to realize a maximum profit? What is the maximum profit?
Found 2 solutions by jim_thompson5910, greenestamps:
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website!
| Trick Ski | Slalom Ski | Max Labor Hrs Available Per Day |
| Fabricating | 8 | 6 | 264 |
| Finishing | 1 | 1 | 40 |
x = number of trick skis sold
y = number of slalom skis sold
both x and y are nonnegative, so  and 
From the first row of the table we see that  because the 8x represents the labor hours for making x number of trick skis, while 6y is the labor hours for making y number of slalom skis. The total (8x+6y) cannot exceed 264 hours, which is why we end up with
Through similar reasoning, the second row gives us this inequality: 
Graph the following system of inequalities
to get this
Let me know if you need me to go into further detail about this part.
The vertex points are:
A = (0, 0)
B = (0, 40)
C = (12, 28)
D = (33, 0)
Each vertex point is found by intersecting the boundary lines. For example, point C is the intersection of the boundary lines 8x+6y = 264 and x+y = 40.
-------------------------------------------------------
"the profit on a trick ski is $40 and the profit on a slalom ski is $50"
40x = profit from only the trick skis (sold at $40 each)
50y = profit from only the slalom skis (sold at $50 each)
P = total profit (both types of skis)
P = 40x + 50y
Plug each vertex point into the profit function
Plug in (x,y) = (0,0)
P = 40x + 50y
P = 40(0) + 50(0)
P = 0
---------------------------------------------
Plug in (x,y) = (0,40)
P = 40x + 50y
P = 40(0) + 50(40)
P = 2000
---------------------------------------------
Plug in (x,y) = (12,28)
P = 40x + 50y
P = 40(12) + 50(28)
P = 1880
---------------------------------------------
Plug in (x,y) = (33,0)
P = 40x + 50y
P = 40(33) + 50(0)
P = 1320
---------------------------------------------
Summary:
Min is P = 0 which occurs at (x,y) = (0,0)
Max is P = 2000 which occurs at (x,y) = (0,40)
To get the max daily profit of $2000 per day, you need to make x = 0 trick skis per day and y = 40 slalom skis per day.
Side note: If both x and y must be greater than zero, then the next highest profit possible is when (x,y) = (12,28). This profit is $1880 per day.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
The other tutor provided a thorough solution to the problem using the standard process: graph the feasibility region and evaluate the profit function at each corner.
In fact that is usually not necessary.
The method described below can usually get you to the solution to this kind of problem faster and with less work.
The given constraints give us the inequalities
And of course x and y have to be zero or positive.
Consider the graphs of the boundary lines of those inequalities. In slope-intercept form they are
A graph....
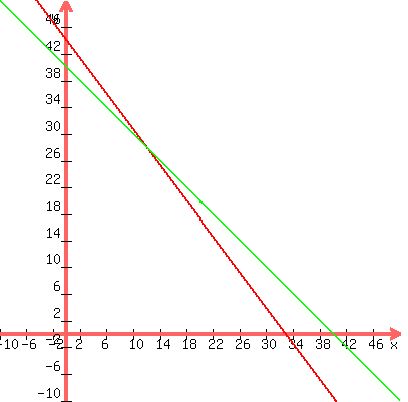
The corners of the feasibility region are (0,0), (0,40), (33,0) and the as yet undetermined point where the two constraint boundary line intersect.
In the standard solution process, you would determine that 4th point and evaluate the profit function at each corner. That is not necessary.
Instead, consider the slope of the profit function. The function is
In slope-intercept form, that is
The maximum profit is going to occur when a line with slope -4/5 just touches a corner of the feasibility region, rather than passing through it.
Comparing the slope of the profit function to the slopes of the two constraint boundary lines, it is clear that the corner of the feasibility region that will yield the maximum profit is (0,40).
So the maximum profit is
|
|
|
