Question 1153867: There are 10 pcs of fruit, 6 were pears. If worker randomly selects 3 pcs for a basket, what is the probability that all were pears?
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There are two ways to solve this problem.
One way is to use the formula P = 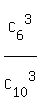 . (1)
The denominator of this formula, . (1)
The denominator of this formula, 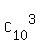 , is the number of combinations of 10 items taken 3 at a time.
In other words, it is the number of all triples that can be formed from 10 pieces of fruits.
The numerator, , is the number of combinations of 10 items taken 3 at a time.
In other words, it is the number of all triples that can be formed from 10 pieces of fruits.
The numerator, 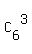 , is the number of all triples of pears that can be formed of 6 pears. , is the number of all triples of pears that can be formed of 6 pears.
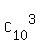 = = 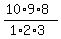 = 120. = 120.
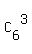 = = 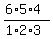 = 20.
Therefore, the probability under the question is P = = 20.
Therefore, the probability under the question is P = 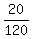 = =  .
Another way is to write
P = .
Another way is to write
P = 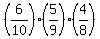 = simplifying = = simplifying = 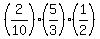 = = 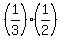 = =  , (2)
which leads to the same answer.
In formula (2), first factor , (2)
which leads to the same answer.
In formula (2), first factor  is the probability to get one pear from 10 fruits;
the factor is the probability to get one pear from 10 fruits;
the factor 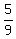 is the probability to get second pear from the remaining 9 fruits;
and the last factor is the probability to get second pear from the remaining 9 fruits;
and the last factor  is the probability to get third pear from the remaining 8 fruits;. is the probability to get third pear from the remaining 8 fruits;.
So, the problem can be solved by any of these two ways, and you should know both.
|
|
|