SOLUTION: The graph of a quadratic function passes through point A (1,8) and has x intercepts 2 and 5. What is the equation of the graph in factored form?

From the condition,  the roots of the quadratic function are x= 2 and x= 5.


Therefore, the quadratic form in factored form is


    y(x) = a*(x-2)*(x-5),


where "a" is an arbitrary (now unknown) real number.


To find the value of "a", use the condition  y(1) = 8,  which leads to the equation


    a*(1-2)*(1-5) = 8,   or


    a*(-1)*(-4) = 8,

    4a = 8,

     a = 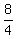 = 2.


The final factorized form of the given quadratic function is


    y(x) = 2*(x-1)*(x-5).