SOLUTION: A line in the coordinate plane has a slope of 4, and a distance of 1 unit from the origin. Find the area of the triangle determined by the line and the coordinate axes

Algebra ->  Graphs -> SOLUTION: A line in the coordinate plane has a slope of 4, and a distance of 1 unit from the origin. Find the area of the triangle determined by the line and the coordinate axes      Log On


   

Question 1153817: A line in the coordinate plane has a slope of 4, and a distance of 1 unit from the origin. Find the area of the triangle determined by the line and the coordinate axes
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!

A line in the coordinate plane has a slope of m=4, and a distance of 1 unit from the origin. => that is a point (1,0)
so, the equation of this line will be:
y-y%5B1%5D=m%28x-x%5B1%5D%29...plug in given data
y-0=4%28x-1%29
y=4x-4
now we know yintercept is at (0,-4)
Find the area of the triangle determined by the line and the coordinate axes

the triangle determined by the line and the coordinate axes is right triangle, and its legs are base and altitude
base is 1 unit long, altitude is 4units long
=> A=%281%2F2%29%2A1%2A4=> A=2


+graph%28+600%2C+600%2C+-10%2C+10%2C+-10%2C+10%2C4x-4%29+

Answer by ikleyn(52879) About Me  (Show Source):
You can put this solution on YOUR website!
.

            The solution by @MathLover1 is  NOT  CORRECT,  since it  DOES  NOT  SATISFY  the condition
            that the distance from the origin to the hypotenuse is 1 unit.

            For the correct solution,  see my post below. 


Let consider this right angled triangle with vertices (0,-4), (0.0), and (1,0).


Its legs have the length 4 and 1; its hypotenuse is 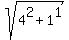 sqrt%284%5E2%2B1%5E1%29 = sqrt%2817%29 long.


We can easy find the height "h" (the altitude) of this triangle, drawn to hypotenuse.


From the area consideration, we have this equation


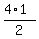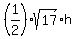    %284%2A1%29%2F2 = %281%2F2%29%2Asqrt%2817%29%2Ah.


It gives  h = 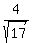4%2Fsqrt%2817%29 = 0.970143.


So, it is not 1 unit, as you see.


It means that the legs of the triangle should be  sqrt%2817%29%2F4  as long, as 1 unit and 4 units of the original triangle.


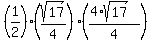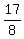So, the area of the seeking triangle is  %281%2F2%29%2A%28sqrt%2817%29%2F4%29%2A%28%284%2Asqrt%2817%29%29%2F4%29%29 = %281%2F2%29%2A%2817%2F4%29 = 17%2F8.    ANSWER



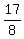ANSWER.  The area of the triangle under the question is  17%2F8.