.
More accurate formulation to this problem is
The probabilities that Macy and Susan hit a target at each shot are 0.6 and 0.5 respectively.
Assume that their result at each shot are independent. If each of them shoots at the target twice,
find the probability that both Macy and Susan hit the target at least once.
Solution
P = P(Macy hits only once of two shots)*P(Susan hits only once of two shots)
+ P(Macy hits twice of two shots)*P(Susan hits only once of two shots) +
+ P(Macy hits only once of two shots)*P(Susan hits twice of two shots) +
+ P(Macy hits twice of two shots)*P(Susan hits twice of two shots) +
= 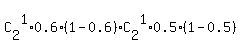 +
+ 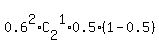 +
+ 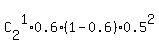 +
+ 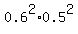 =
=
=
=  +
+ 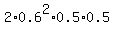 +
+ 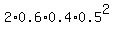 +
+ 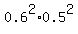 = 0.63. ANSWER
= 0.63. ANSWER