SOLUTION: Ship A sailing due north at 6 km/h sights ship B sailing northwest 4 km away and sailing due east at 5 km/h. How close will the two ships pass if neither alters course or speed?

Introduce the coordinate plane (x,y) in a way that ship's A initial location is the origin of the coordinate plane;
x-axis is directed East and y-axis is directed North.


Then the initial location of the ship B is the point (,).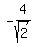


The ship A moves along y-axis, according to equation y = 6*t, where t is the time in hours.

So, the ship A location in time on the coordinate plane is A = (0,6t).


Ship B moves parallel to x-axis, according to equation x = 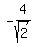 + 4*t, where t is the time in hours.

So, the ship B location in time on the coordinate plane is B = (,).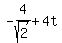


Now find the square of distance between the points A and B


    d^2 =  + .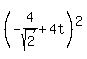


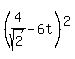Simplify


    d^2 =  +  = .


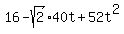Thus you have this quadratic function of "t", and you need to find its MINIMUM.


Use the formulas for the vetex of the quadratic function/parabola


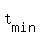     = " (-b/(2a)) " =  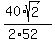=  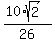=  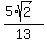= 0.5439 hours.


To find the square of the minimal distance, substitute t = 0.5439 into the formula (1). You will get


    d^2 = 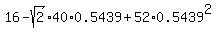 = 0.6154.


Hence d = 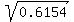 = 0.7845.


ANSWER.  The minimal distance between the ships will be 0.7845 kilometers.