Question 1153676: Select the option for "?" that continues the pattern in each question.
58
3, -6, 12, 4, 20, ?
13
14
6
16
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
These numbers are related in the following way, beginning with  : :
First, we subtract  to get to get  : :

Next, we add  : :

To get from  to to  , we subtract , we subtract  : :
 , and , and
to get from  to the final number of to the final number of  , we must add , we must add  : :

We need to examine the numbers that we add/take away in the sequence to find a pattern so we can predict the next number.
So, let's look at the relationship between the numbers we added and subtracted to get from  to to  , from , from 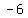 to to  , and so on. , and so on.
First, we subtracted  , then added , then added  , then subtracted , then subtracted  , then added , then added  . .
Think of ways in which the numbers  , ,  , ,  , and , and  are related. are related.
If I start with  , I have to multiply by , I have to multiply by  to get to get  : :

To get from the next number,  , to the fourth in the sequence, , to the fourth in the sequence,  , I must multiply by , I must multiply by  again: again:

Now, we know the relationship between  and and  , and the relationship between , and the relationship between  and and  . .
We still need to figure out why the pattern moves from adding  to subtracting to subtracting  . To do this, I returned to my idea of multiplying by . To do this, I returned to my idea of multiplying by  , which grouped our numbers as follows: , which grouped our numbers as follows:
 was related to was related to  , and , and  was related to was related to  . .
We can see that  . .
So, let's say  is " is " ." The relationship between the numbers in the original sequence can be summed up as follows: ." The relationship between the numbers in the original sequence can be summed up as follows:
First number in the sequence  , ,  , , 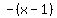 , , 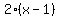 . .
Let's plug in  as the as the  number in the sequence and number in the sequence and  as as  to test our pattern: to test our pattern:




If we put those answers in order, we have  , ,  , ,  , ,  , ,  : the original sequence! : the original sequence!
Using the pattern we found in that equation, we can predict that the next number in the sequence would be related to  by subtracting by subtracting  , where , where 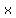 still equals still equals  , since in order to get , since in order to get  after after  we had to subtract we had to subtract  from from  . .
So, 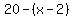 becomes becomes  . .
so, answer is: 
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor found "A" pattern that produces the given sequence of numbers and used that pattern to determine the next number -- which was one of the given answer choices.
That is all very nice.... But there is no way of knowing that the pattern they found is the "CORRECT" pattern.
And in fact ANY problem like this is invalid if you are required to find a "right" answer; ANY next number would make a valid sequence.
Spend as much (or as little) time as you want trying to find a pattern; but realize that any pattern you find might not be "right" and might give the "wrong" next number.
|
|
|