|
Question 1153658: My teacher asks, "The difference between a polynomial or rational equation and polynomial or rational inequality"
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52817)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An equation has the EQUALITY sign " = " between two parts (between two expressions).
An inequality has the INEQUALITY sign " < ", or " <= ", or " > ", or " >= " between two parts (between two expressions).
Happy learning (!)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! The difference between a polynomial or rational equation and polynomial or rational inequality:
An equation has the EQUALITY sign " = " between two parts (between two expressions).
A polynomial function is a function of the form:
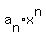 +....+ +....+ where where  is a non-negative integer and is a non-negative integer and 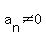
A polynomial of degree  has at most has at most  real zeros and real zeros and 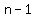 turning points. turning points.
The difference between a polynomial or rational equation and polynomial or rational inequality:
A polynomial function is a function of the form:
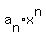 +....+ +....+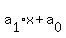 where where  is a non-negative integer and is a non-negative integer and 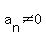
A polynomial of degree  has at most has at most  real zeros and real zeros and 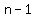 turning points. turning points.
First, the end behavior of a polynomial is determined by its 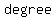 and the and the 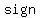 of the of the   . .
The degree of a polynomial function determines the end behavior of its graph. If the degree of a polynomial is even, then the end behavior is the same in both directions. If the degree of a polynomial is odd, then the end behavior on the left is the opposite of the behavior on the right.
A rational equation is just a quotient of two polynomials. Quotient here just means “fraction.” So, if 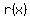 is a rational expression, then it can be written as: is a rational expression, then it can be written as:
 where where 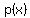 and and 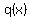 are both polynomials. are both polynomials.
A rational function may have a 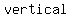 asymptote whenever asymptote whenever  which which 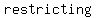 the the 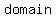 of the function. of the function.
The graphs of rational functions may have vertical asymptotes only where the denominator is zero, and a 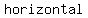 asymptote (a horizontal line that the graph approaches as the input increases or decreases without bound). asymptote (a horizontal line that the graph approaches as the input increases or decreases without bound).
The end behavior of the graph of a rational function is determined by the  of the of the 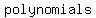 in the in the 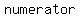 and and  . .
The graphs of rational functions may have vertical asymptotes only where the denominator is zero.
Two differences difference between a 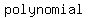 or or 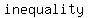 : :
First, an inequality has the INEQUALITY sign " < ", or " <= ", or " > ", or " >= " between two parts (between two expressions).
A polynomial inequality (PI) can 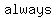 be replaced by a PI with one side zero. That is, be replaced by a PI with one side zero. That is,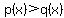 is the same as is the same as 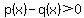 . .
A rational inequality (RI)   , because you , because you 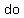   the the  of the of the  ; ;
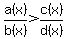 can not safely be replaced by can not safely be replaced by

because 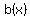 and/or and/or 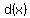 might change signs unexpectedly. might change signs unexpectedly.
|
|
|
| |