SOLUTION: In a round robin tournament, each team plays every other team once. The formula G=n(n-1)/2 gives the number of games G that must be scheduled for n teams. Will the number of game

If there are n teams, G(n) = n(n-1)/2



If there are m=2n teams, G(m) = m(m-1)/2 = 2n(2n-1)/2 = n(2n-1) games



The difference is





So, NO, the number of games does not double, it increasses by  when n doubles.

 



Example:



G(6) = 6(5)/2 = 15

G(12) = 12(11)/2 = 66



The difference is 66-15 = 51  

and  for n=6: n(3n-1)/2 = 6(3*6-1)/2 = 6(17)/2 = 51, as derived above.



============

To the student:  sorry just noticed your additional question in the 'thank you' message:  it means when you double the number of teams, the number of games goes up by 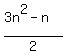 or we can say (roughly) "if the number of teams doubles, the number of games needed goes up on the order of ".  In the example I gave, n=6, G(n)=15  then I doubled the number of teams to 12 and showed G(12) = 66 so you can see the number games went up by a factor of 66/15 or 4.4.  4.4 is _roughly_ (on the same order of magnitude as)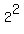 



Forgot to say... so yes, for doubling teams, you roughly quadruple the # of games needed for the RR.