Question 1153574: The graph of
f(x) = -1/2 (1/6)exponent is x-7
+9 is shifted left 7 units, stretched vertically by a factor of 6, reflected about the x-axis, and then shifted downward 9 units. What is the equation of the new function, g(x)?
g(x) =
State the y-intercept of
g(x).
(x, y) =
State the domain and range of
g(x).
(Enter your answers using interval notation.)
domain
range
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! SHIFTS OF THE PARENT FUNCTION:

For any constants  , ,  and and  , the function , the function

-is stretched vertically by a factor of  if if 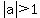
-is compressed vertically by a factor of  if if 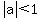
-has a y-intercept of ( , , ) )
-shifts the parent function vertically  units, in the same direction of the sign of units, in the same direction of the sign of 
-horizontally  units, in the opposite direction of the sign of units, in the opposite direction of the sign of 
-the y-intercept becomes ( , ,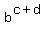 ) )
-the horizontal asymptote becomes 
-the range becomes ( , , ). ).
-the domain, ( , , ), remains unchanged ), remains unchanged
in your case we have 
the equation of the new function,  : :
- is shifted left 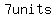 , so we have , so we have


-stretched vertically by a factor of , so we have , so we have


-reflected about the  -axis, so we have -axis, so we have


and then shifted downward  units, so we have units, so we have


State the y-intercept of  . .
( , ,  ) =( ) =( , , ) )
the domain and range of  : :
the range becomes ( , , ) )
the domain, ( , , ) )

|
|
|