SOLUTION: Three circles are mutually tangent to one another externally. Their centers are connected forming a triangle whose sides are 16 cm, 20 cm, and 24 cm. Find the area of the largest c

Let "a", "b" and "c" be the radii of these circles.


Notice that each segment connecting the centers of any two of the three given circles has the length equal to the sum of the related radii.

Therefore, we have these three equations for 3 unknowns "a", "b" and "c"


    a + b = 16,     (1)

    a + c = 20,     (2)

    b + c = 24.     (3)


To solve the system, add all three equations (1), (2) and (3).

You will get 


    2a + 2b + 2c = 16 + 20 + 24,

    2*(a + b + c) = 60.

hence,

    a + b + c = 30.    (4)


To find "a", subtract equation (3) from equation (4). You will get  a = 30-24 = 6.

Then from (1),  b = 16-6 = 10  and from (2)  c = 20-6 = 14.


The area of the largest circle is   = 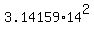 = 615.75 cm^2    (approximately).    ANSWER