.
The problem asks which NOMINAL annual interest compounded monthly is equivalent to the annual interest of 8% compounded annually.
Let x be the nominal interest rate under the question.
Then the account grows from month to month with the effective growing coefficient 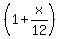 .
Thus the equation to find x is THIS
.
Thus the equation to find x is THIS
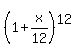 = 1 + 0.08, or
= 1 + 0.08, or
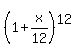 = 1.08.
From the equation
= 1.08.
From the equation
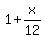 = 1.08^(1/12) = 1.006434.
and finally you get
= 1.08^(1/12) = 1.006434.
and finally you get
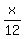 = 1.006434 - 1 = 0.006434.
Therefore, x = 12*0.006434 = 0.0772.
Thus the equivalent (or effective) nominal annual interest rate is 7.72%.
ANSWER. NOMINAL annual interest compounded monthly, equivalent to the annual interest of 8% compounded annually, is 7.72%.
Or, in more compact form, 8% annual interest compound annually, is equivalent to 7.72% annual interest compound monthly.
= 1.006434 - 1 = 0.006434.
Therefore, x = 12*0.006434 = 0.0772.
Thus the equivalent (or effective) nominal annual interest rate is 7.72%.
ANSWER. NOMINAL annual interest compounded monthly, equivalent to the annual interest of 8% compounded annually, is 7.72%.
Or, in more compact form, 8% annual interest compound annually, is equivalent to 7.72% annual interest compound monthly.