Question 1153034: Find the equation of the tangent to the curve x^2y-x=y^3-8 at x=0.
Found 2 solutions by Alan3354, Edwin McCravy:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! Find the equation of the tangent to the curve x^2y-x=y^3-8 at x=0.
----------------
I did this, but lost it before it was posted.
=====
@ x = 0, y = 2
----
Differentiate implicitly and find the slope.
Slope = -1/12
---> y = (-x/12) + 2
-----------------------------
email via the TY note if you need help.
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website! x^2y-x=y^3-8 at x=0
Substituting x=0,
So the point of tangency is (0,2), and we want the equation of the
green line below:
We find the slope of the tangent line, which is the
same as the derivative at that point: So we find
the derivative implicitly, i.e., without solving for
the independent variable y:
We substitute x=0 and y=2 and solve for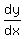 
That's the slope of the tangent line at (0,2), which is
the green line. So
Since the point of tangency is the y-intercept (0,2), we can just
use:
with
Edwin
|
|
|
