Question 1153004: Suzie has a collection of coins: a penny, a dime, a nickel, and a quarter. If she picks two coins out at a time, what are all of the possible outcomes?
Answer by ikleyn(52824)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I will code the coins by the first letter of their names:
P for penny;
N for nickel;
D for dime;
Q for quarter.
Then all outcomes are these pairs
PN, PD, PQ, ND, NQ, DQ.
In all, there are 6 pairs.
Notice that in Suzie's collection, there is only ONE coin in each nomination.
Therefore, the pairs PP, NN, DD, QQ do not exist.
Also, the order of coins in pairs does not matter.
Thus the number of outcomes is equal to the number of all combinations of 4 items taken 2 at a time
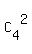 = = 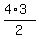 = 2*3 = 6. = 2*3 = 6.
----------------
This problem introduces you to the notion/conception of COMBINATIONS.
On Combinations, see introductory lessons
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- OVERVIEW of lessons on Permutations and Combinations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Combinatorics: Combinations and permutations".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|