SOLUTION: let x and y are acute angles, tan(x). tan(y) =1, tan(x) - tan(y) = 2 × sqrt(3) prove that x=5y

Algebra ->  Graphs -> SOLUTION: let x and y are acute angles, tan(x). tan(y) =1, tan(x) - tan(y) = 2 × sqrt(3) prove that x=5y       Log On


   

Question 1152875: let x and y are acute angles, tan(x). tan(y) =1,
tan(x) - tan(y) = 2 × sqrt(3) prove that x=5y
Answer by ikleyn(52898) About Me  (Show Source):
You can put this solution on YOUR website!
.

Let x be the greater of the two given acute angles, and let y be the smaller.


Then, first, the equality  tan(x)*tan(y) = 1  implies that

    x + y = 90°.         (1)


Second, 

    tan(x-y) = 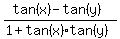%28tan%28x%29-tan%28y%29%29%2F%281+%2B+tan%28x%29%2Atan%28y%29%29 = 

         substitute given values for the numerator and denominator to get

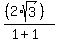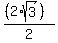              = %28%282%2Asqrt%283%29%29%29%2F%281%2B1%29 = %28%282%2Asqrt%283%29%29%29%2F2 = sqrt%283%29,

which implies  

    x - y = 60°.           (2)


From equations (1) and (2), by adding, you get

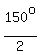    2x = 90° + 60° = 150°;   hence,  x = 150%5Eo%2F2 = 75°.


Finally, substituting this value of x into (1), you get  y = 15°.


So, under the given conditions,  x = 75°  and  y = 15°.


In particular,  x = 5y.

Solved.