Question 1152851: III. Given the linear system
2x1 + 3x2 - x3 = 0
x1 - 4x2 + 5x3 = 0
(a) Verify that x1 = 1, x2 = -1, x3 = - 1 is a solution.
(b) Verify that x1 = -2, x2 = 2, x3 = 2 is a solution.
(c) Adding the corresponding x-values of the solution in parts (a) and (b) gives x1 = -1, x2 = 1, x3 = 1. Is this a solution to the linear system?
(d) Multiply each of the x-values in part (a) by 3. Are the resulting values a solution to the linear system?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!


(a) Verify that  , ,  , ,  is a solution. is a solution.
 ......substitute given values ......substitute given values



 -> ->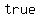
and




 -> ->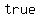
so,  , ,  , ,  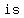 a solution a solution
(b) Verify that  , ,  , , is a solution. is a solution.
 ......substitute given values ......substitute given values



 -> ->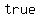
and




 -> ->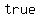
=> , ,  , ,  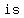 a solution a solution
(c) Adding the corresponding x-values of the solution in parts (a) and (b) gives
 , ,  , , 
Is this a solution to the linear system?
 ......substitute given values ......substitute given values



 ->true ->true
and




 ->true ->true
=> , ,  , ,  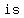 a solution to the linear system a solution to the linear system
(d) Multiply each of the x-values in part (a) by 3. Are the resulting values a solution to the linear system?
 , ,  , , 
 ......substitute given values ......substitute given values



 -> ->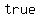
and




 -> ->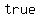
=>the resulting values  solution to the linear system solution to the linear system
|
|
|