Question 1152786: A committee of 6 U.S. senators is to be formed with 3 Democrats and 3 Republicans. In how many ways can this be done if there are 61 Democratic senators and 39 Republican senators?
Found 2 solutions by jim_thompson5910, ikleyn:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We will use the combination function

to count the number of ways to select members. We use the combination function (not the permutation function) because order does not matter when selecting a committee. Any member does not outrank another, and there are no special positions. All that matters is the group as a whole rather an any particular individual.
Your book may use notation that looks like  instead of instead of  , but its the same thing. , but its the same thing.
The exclamation marks represent factorials. Writing something like 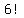 means means  so we start at 6 and count our way down to 1 multiplying along the way. so we start at 6 and count our way down to 1 multiplying along the way.
-----------------------------------------------
Note how something like  is fully contained inside of the expression for is fully contained inside of the expression for 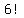
This means, 
In short, 
This will come in handy later on. Specifically the lines where I write "use the factorial trick" (see below). This is to cancel out factorials that would otherwise be massively large numbers.
-----------------------------------------------
For the Democrats, we have n = 61 people to choose from and r = 3 slots to fill.
Use the combination function to figure out how many ways there are to do this.

 Replace n with 61, replace r with 3 Replace n with 61, replace r with 3
 Use the factorial trick. We started at 61 and stop at 58 because of the 58! in the denominator. Use the factorial trick. We started at 61 and stop at 58 because of the 58! in the denominator.
 We have these highlighted terms pair up We have these highlighted terms pair up
 and cancel out. A much simpler expression is left over and cancel out. A much simpler expression is left over
 Expand out Expand out 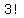 to get to get 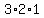
At this point, we have three numbers multiplied in the numerator. It is not a coincidence this lines up with r = 3. So another shortcut is to start with the number n = 61 and count down by 1 until you have r = 3 items to multiply out in the numerator. Then you divide over 3! = 3*2*1
Let's simplify



There are 35990 ways to pick the Democrats.
We'll use this number later, so let A = 35990
-----------------------------------------------
Repeat for the Republicans
n = 39
r = 3



 Use the factorial trick Use the factorial trick
 Terms pair up Terms pair up
 and cancel out and cancel out
 Since r = 3, we have 3 numbers multiplied in the numerator. We started at n = 39 and counted down by 1 each time. Since r = 3, we have 3 numbers multiplied in the numerator. We started at n = 39 and counted down by 1 each time.
 Expand out Expand out 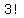 to get to get 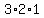


Let B = 9139 represent the number of ways to pick the Republicans.
-----------------------------------------------
To summarize what we found so far,
A = 35990 is the number of ways to pick the Democrats
B = 9139 is the number of ways to pick the Republicans
So,
A*B = 35990*9139 = 328,912,610 is the number of ways to pick the entire committee.
Order does not matter.
This number is very close to 329 million.
Answer by ikleyn(52790)   (Show Source): (Show Source):
|
|
|