SOLUTION: Two vertices of a triangle are A(3,6) and B(7,12). a) Find the equation of line AB. b) Find the equation of the perpendicular bisector of line AB. c) Given that AC is perpendi

Algebra ->  Test -> SOLUTION: Two vertices of a triangle are A(3,6) and B(7,12). a) Find the equation of line AB. b) Find the equation of the perpendicular bisector of line AB. c) Given that AC is perpendi      Log On


   

Question 1152746: Two vertices of a triangle are A(3,6) and B(7,12).
a) Find the equation of line AB.
b) Find the equation of the perpendicular bisector of line AB.
c) Given that AC is perpendicular to AB and the equation of line BC is y=-5x+47,find the coordinates of C.

Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
Two vertices of a triangle are+A(3,6) and B(7,12).

a) Find the equation of line AB.
y=mx%2Bb
use given points to find a slope:
m=%28y%5B2%5D-y%5B1%5D%29%2F%28x%5B2%5D-x%5B1%5D%29=%2812-6%29%2F%287-3%29=6%2F4=3%2F2
now use point-slope formula to find equation:
y-y%5B1%5D=m%28x-x%5B1%5D%29
y-6=%283%2F2%29%28x-3%29
y-6=%283%2F2%29x-3%283%2F2%29
y=%283%2F2%29x-9%2F2%2B6
y=%283%2F2%29x-9%2F2%2B12%2F2
y=%283%2F2%29x%2B3%2F2->the equation of line AB


b) Find the equation of the perpendicular bisector of line AB.
the equation of the perpendicular bisector of line AB will have a slope negative reciprocal which is
m%5Bp%5D=-1%2Fm=-1%2F%283%2F2%29=-2%2F3
then, use point-slope formula to find equation:
y-y%5B1%5D=m%5Bp%5D%28x-x%5B1%5D%29
y-6=-%282%2F3%29%28x-3%29
y-6=-%282%2F3%29x-3%28-2%2F3%29
y-6=-%282%2F3%29x%2B6%2F3
y-6=-%282%2F3%29x%2B2
y=-%282%2F3%29x%2B2%2B6
y=-%282%2F3%29x%2B8
c) Given that AC is perpendicular to AB and the equation of line BC is y=-5x%2B47,find the coordinates of C.
the coordinates of C will be the coordinates of intersection point, or solution of
y=-%282%2F3%29x%2B8
y=-5x%2B47
---------------------------left sides are equal, then
-%282%2F3%29x%2B8=-5x%2B47.............solve for x
-%282%2F3%29x%2B5x=-8%2B47
-2x%2F3%2B15x%2F3=39
13x%2F3=39
13x=39%2A3
x=%2839%2F13%29%2A3
x=3%2A3
x=9
find y:
y=-5%2A9%2B47
y=2
intersection point is at: (9,2)




Answer by MathTherapy(10555) About Me  (Show Source):
You can put this solution on YOUR website!

Two vertices of a triangle are A(3,6) and B(7,12).
a) Find the equation of line AB.
b) Find the equation of the perpendicular bisector of line AB.
c) Given that AC is perpendicular to AB and the equation of line BC is y=-5x+47,find the coordinates of C. 
Slope of a line as well as a point on the line can be used to form a linear equation

From a), it's determined that the slope of AB, or 

Perpendicular slopes are negative reciprocals of each other. So, with the slope (m), in a) being 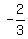3%2F2, the slope (m) in b) will be -+2%2F3

b) To form an equation, one needs a slope and a point.

   Slope for b): 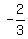-+2%2F3

   Point for b): the MIDPOINT of line AB, in a) can be derived by using the MIDPOINT formula and the coordinates of AB, as follows: 

Along with the slope (m), and the point (5, 9), the equation of the perpendicular bisector of line AB is: 

In c), AC CANNOT be perpendicular to AB.