Question 1152412: A rectangular piece of cardboard, whose area is 396 square centimeters, is made into an open box by cutting a 2-centimeter square from each corner and turning up the sides. If the box is to have a volume of 504cubic centimeters, what size cardboard should you start with?
Answer by ikleyn(52901)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x and y be the values under the question, i.e. dimensions of the original piece of cardboard.
The height of the box is 2 cm;
the area of the base of the box is equal to its volume divided by the height
area of the base of the box = 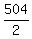 = 252 cm^2.
It gives you your first equation
(x-2*2)*(y-2*2) = 252, or
(x-4)*(y-4) = 252. (1)
The second equation is for the surface area of the box
(x-4)*(y-4) + 2*(x-4) + 2*(y-4) = 396 - 4*(2*2) cm^2, or
(x-4)*(y-4) + 2*(x-4) + 2*(y-4) = 380. (2)
It is your second equation.
Simplify them.
In the left side of (2), replace (x-4)*(y-4) by 252, based on (1).
You will get then instead of (2)
252 + 2*(x-4) + 2*(y-4) = 380, or
2*(x-4) + 2*(y-4) = 380 - 252 = 128,
(x-4) + (y-4) = 64.
So, the sum (x-4) + (y-4) = 64, while the product (x-4)*(y-4) = 252.
Thus (x-4) and (y-4) are the roots of the quadratic equation t^2 - 64t + 252 = 0.
Hence, = 252 cm^2.
It gives you your first equation
(x-2*2)*(y-2*2) = 252, or
(x-4)*(y-4) = 252. (1)
The second equation is for the surface area of the box
(x-4)*(y-4) + 2*(x-4) + 2*(y-4) = 396 - 4*(2*2) cm^2, or
(x-4)*(y-4) + 2*(x-4) + 2*(y-4) = 380. (2)
It is your second equation.
Simplify them.
In the left side of (2), replace (x-4)*(y-4) by 252, based on (1).
You will get then instead of (2)
252 + 2*(x-4) + 2*(y-4) = 380, or
2*(x-4) + 2*(y-4) = 380 - 252 = 128,
(x-4) + (y-4) = 64.
So, the sum (x-4) + (y-4) = 64, while the product (x-4)*(y-4) = 252.
Thus (x-4) and (y-4) are the roots of the quadratic equation t^2 - 64t + 252 = 0.
Hence,  = = 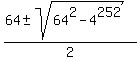 = = 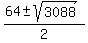 = = 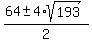 = = 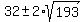 .
It gives x-4 = .
It gives x-4 =  , x = , x = 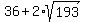 = 63.785 cm.
y-4 = = 63.785 cm.
y-4 =  , y = , y = 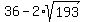 = 8.215 cm.
CHECK. Equation (1) : (x-4)*(y-4) = (63.785 -4)*(8.215-4) = 251.994 = 252 cm^2;
Equation (2) : (x-4)*(y-4) + 2*(x-4) + 2*(y-4) = (63.785 -4)*(8.215-4) + 2*(63.785 -4) + 2*(8.215-4) = 379.994 = 380 cm^2.
ANSWER. The dimensions are x = = 8.215 cm.
CHECK. Equation (1) : (x-4)*(y-4) = (63.785 -4)*(8.215-4) = 251.994 = 252 cm^2;
Equation (2) : (x-4)*(y-4) + 2*(x-4) + 2*(y-4) = (63.785 -4)*(8.215-4) + 2*(63.785 -4) + 2*(8.215-4) = 379.994 = 380 cm^2.
ANSWER. The dimensions are x = 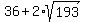 = 63.785 cm and y = = 63.785 cm and y = 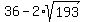 = 8.215 cm. = 8.215 cm.
Solved.
----------------
If you want to see many other similar solved problems, look into the lesson
- Making a box from a piece of cardboard
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic
"Dimensions and the area of rectangles and circles and their elements".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|