Question 1152187: A quadratic pattern has a second term equal to -1,a third equal to -6 and a fifth term equal to -14.Calculate the second difference of this quadratic pattern.
Hence,or otherwise ,calculate the first term of the pattern.
Found 3 solutions by MathLover1, MathTherapy, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A quadratic pattern has:
a second term equal to  , ,
a third equal to 
a fifth term equal to 
Calculate the second difference of this quadratic pattern.
Hence,or otherwise ,calculate the first term of the pattern.
If the sequence is quadratic, the  term is of the form term is of the form

use given terms to calculate  , , , and , and 
 ....if ....if  given given 

 ........solve for ........solve for 
 ..........eq.1 ..........eq.1
 ....if ....if  given given 

 ........solve for ........solve for 
 ..........eq.2 ..........eq.2
 ....if ....if  given given 

 ........solve for ........solve for 
 ..........eq.3 ..........eq.3
from eq.1 and eq.2 we have
 ........solve for ........solve for 


 ................eq.1a ................eq.1a
from eq.1 and eq.3 we have
 ........solve for ........solve for 



 ..............eq.2a ..............eq.2a
from eq.1a and eq.2a we have:
 ......solve for ......solve for 



 .......cross multiply .......cross multiply




go to  ................eq.1a, substitute ................eq.1a, substitute 





go to  ..........eq.1, substitute ..........eq.1, substitute  and and 





so,  , ,  , and , and 
your quadratic pattern is:

now we can calculate first term:



Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website! A quadratic pattern has a second term equal to -1,a third equal to -6 and a fifth term equal to -14.Calculate the second difference of this quadratic pattern.
Hence,or otherwise ,calculate the first term of the pattern.
This person makes these problems so, so, COMPLEX and more time-consuming than is necessary.
After substituting each term into the quadratic pattern formula:  , you should get the following system of equations:
4A + 2B + C = - 1 ------ eq (i)
9A + 3B + C = - 6 -------eq (ii)
25A + 5B + C = - 14 ----- eq (iii)
5A + B = - 5 ------- Subtracting eq (i) from eq (ii) ----- eq (iv)
16A + 2B = - 8 ----- Subtracting eq (ii) from eq (iii) --- eq (v)
- 10A - 2B = 10 ---- Multiplying eq (iv) by - 2 ----- eq (vi)
6A = 2 ----- Adding eqs (v) & (vi) , you should get the following system of equations:
4A + 2B + C = - 1 ------ eq (i)
9A + 3B + C = - 6 -------eq (ii)
25A + 5B + C = - 14 ----- eq (iii)
5A + B = - 5 ------- Subtracting eq (i) from eq (ii) ----- eq (iv)
16A + 2B = - 8 ----- Subtracting eq (ii) from eq (iii) --- eq (v)
- 10A - 2B = 10 ---- Multiplying eq (iv) by - 2 ----- eq (vi)
6A = 2 ----- Adding eqs (v) & (vi)

 ----- Substituting ----- Substituting  for A in eq (iv) for A in eq (iv)


 --- Substituting --- Substituting  for A, and for A, and 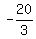 for B in eq (i) for B in eq (i)

 - 12 + C = - 1
C = - 1 + 12
C = 11
- 12 + C = - 1
C = - 1 + 12
C = 11
  ==============
Although not needed, if you're curious, the quadratic sequence,
==============
Although not needed, if you're curious, the quadratic sequence,  becomes: becomes: 
Answer by greenestamps(13215)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You have received two responses to your question showing algebraic methods for obtaining the quadratic function that produces the given 2nd, 3rd, and 5th terms; and from that quadratic function you can determine the second difference and the first term.
Note that the question does not require you to find the quadratic function; it only asks you to find the second difference and the first term.
Here is how you can do that, using the method of finite differences -- without having to determine the formula for the quadratic sequence.
We know the sequence is quadratic and therefore there is a common second difference. Let that common difference be d; and let the missing 1st and 4th terms be a and b. Using the method of finite differences with the information we have at the beginning gives us the following diagram showing the original sequence and the first and second differences:
a -1 -6 b -14
x -5 y z
d d d
We can use the method of finite differences to get expressions for x, y, and z in terms of d:
-5-x = d --> x = -d-5
y-(-5) = d --> y+5 = d --> y = d-5
z-y = d --> z-(d-5) = d --> z = 2d-5
Our finite differences diagram now looks like this:
a -1 -6 b -14
-d-5 -5 d-5 2d-5
d d d
We can now get an expression for a in terms of d:
-1-a = -d-5 --> a = d+4
We can also get TWO DIFFERENT equations relating b and d; that will allow us to solve for d.
-14-b = 2d-5
b+6 = d-5
Add the two equations: -8 = 3d-10 --> d = 2/3
We have the answer to one of the two questions: the common second difference is d = 2/3.
And we have an expression for the first term a in terms of d: a = d+4 = 2/3+4 = 14/3.
ANSWERS:
the second difference for the quadratic sequence is 2/3
the first term of the sequence is 14/3
|
|
|