SOLUTION: How many distinguishable permutations are there of the letters in WOODCOCK?

The word "WOODCOCK" has 8 letters.


Of them, letter "O" has the multiplicity of 3;

         letter "C" has the multiplicity of 2;

         the rest of the letters are unique.


Therefore, the number of all distinguishable permutations (they are also called "distinguishable arrangements") is


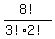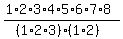       =  = 3360.    ANSWER


8! counts the number of all possible permutations of 8 letters.


3! in the denominator stays to account for repeating letter "O".


2! in the denominator stays to account for repeating letter "C".