SOLUTION: If p and q are the fourth and the seventh terms respectively of an arithmetic series, 1 determine the common difference 2 the sum to the ten terms of the series.

Between the 4-th and 7-th terms of any AP, there are 3 gaps of equal size.

Therefore, the common difference is  d = 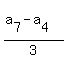 = .        ANSWER

Notice that    is the 4-th term of the AP from the beginning,

      while    is the 4-th term of the AP from the end (from the ending term  ).



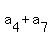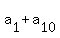Therefore,   =  = p + q.    (*)



    It is a general property of any AP:  


       the sum of the terms equally remoted from the beginning and the end of an AP
       is equal to the sum of the first and the last its terms.



From the other side,  the sum of any AP is equal to the sum of the first and the last terms, divided by 2 and multiplied 
by the number of terms.


Therefore,


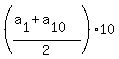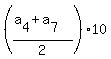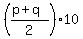       +  +  + . . . +  =  =  =  = 5*(p+q).     ANSWER