Question 1152008: There are five people in a room. Each person shakes the hand of every other person exactly one. How many hands shakes are exchanged
Found 3 solutions by MathLover1, greenestamps, ikleyn:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is a more sophisticated method for counting the number of handshakes; it is especially useful when the number of people is large.
Suppose the number of people is n. Then each of the n people shakes hands with each of the other (n-1) people, making a total of n*(n-1) handshakes.
But when you count all of the handshakes by all the people in that way, you count each distinct handshake twice; so the actual number of handshakes is (n*(n-1))/2.
In this problem, with 5 people, that gives you (5*(5-1))/2 = (5*4)/2 = 10.
Of course, adding 4+3+2+1 is faster than that.... But if the number of people were 79 instead of 4, you wouldn't want to be adding 78+77+76+...+3+2+1 to find the number of handshakes.
Answer by ikleyn(52878)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Standard (but not unique (!) ) solution to this problem is as follows.
Each person makes (n-1) handshakes, so your first intention is to answer n*(n-1) handshakes, in all.
But be careful (!)
By counting in this way, we count each handshake twice, for every of the two hand shakers.
Therefore, we must divide n*(n-1) by 2, and then we come to the correct answer:
the number of handshakes is 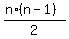 . ANSWER . ANSWER
Solved.
-----------------
It is classic problem (!)
MEMORIZE its solution (!)
|
|
|