Question 1151815: Solve for the general solution with exact answers
2cos^2(x)-3cos(x)=-1
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
2cos^2(x) - 3cos(x) = -1.
The way to solve such equations is to introduce new variable y = cos(x).
Then your equation takes the form
2y^2- 3y = -1, or
2y^2 - 3y + 1 = 0.
Apply the quadratic formula
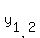 = = 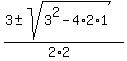 = = 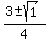 = = 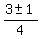 .
So, there are two roots
1) y = .
So, there are two roots
1) y = 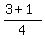 = = 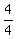 = 1.
Recall that y = cos(x). So, cos(x) = 1.
It implies x = = 1.
Recall that y = cos(x). So, cos(x) = 1.
It implies x =  , k = 0, +/-1, +/-2, . . .
2) y = , k = 0, +/-1, +/-2, . . .
2) y =  = = 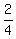 = =  .
Recall that y = cos(x). So, cos(x) = 1/2.
It implies x = .
Recall that y = cos(x). So, cos(x) = 1/2.
It implies x = 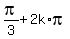 , k = 0, +/-1, +/-2, . . .
or x = , k = 0, +/-1, +/-2, . . .
or x = 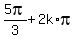 , k = 0, +/-1, +/-2, . . .
ANSWER. x = , k = 0, +/-1, +/-2, . . .
ANSWER. x =  , k = 0, +/-1, +/-2, . . . or
x = , k = 0, +/-1, +/-2, . . . or
x = 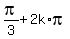 , k = 0, +/-1, +/-2, . . . or
x = , k = 0, +/-1, +/-2, . . . or
x = 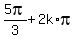 , k = 0, +/-1, +/-2, . . . , k = 0, +/-1, +/-2, . . .
Solved.
---------------
If you want to see many other similar solved problems, look into the lessons
- Solving simple problems on trigonometric equations
- Solving typical problems on trigonometric equations
- Solving more complicated problems on trigonometric equations
- Solving advanced problems on trigonometric equations
- Challenging problems on trigonometric equations
- OVERVIEW of lessons on calculating trig functions and solving trig equations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Trigonometry: Solved problems".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|