Question 1151776: solve for x:
Answer by ikleyn(52756)   (Show Source):
You can put this solution on YOUR website! .
The point is that 2 is the maximal value of the given function.
It can be proved by standard method of Calculus:
by taking the derivative, equating it to zero, and then solving the associated equation.
In this post I will show you another way, which quickly leads to the answer.
(1) First notice that cos(x)+sin(x) has the maximum value of  at x =  . // Every Calculus student must know it (!)
(2) At this value of x, sin(2x) = 1 and, therefore, sin(2x)+1 = 2. It is maximum value of sin(2x)+1.
(3) Therefore, at x=  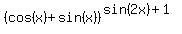=  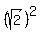= 2.
(4) At all other values of x in the interval [ , ), cos(x) + sin(x) is less than
and sin(2x)+1 is less than 2; therefore, the entire function 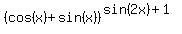is strictly less than 2.
(5) Thus, the only solution to the original equation in the interval [,) is x= .
Solved.
|
|
|
