Question 1151765: a family drove to a resort at an avrage speed of 3o mph and later returned over the same road at an average speed of 45 mph. find the distance to the resort if the total driving time was 8 hours
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52829)   (Show Source):
You can put this solution on YOUR website! .
Let "d" be the distance to the resort.
Then the driving time of 8 hours is the sum of the driving time to there, 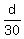 hours, and the driving time back,  hours:
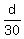+ = 8 hours. (1)
It is your basic equation to find the unknown value "d".
To solve it, multiply both sides of the equation by 90. You will get
3d + 2d = 8*90
5d = 720
d = 720/5 = 144.
ANSWER. One way distance is 144 miles.
Solved.
-----------------
The solution is based on using the "time" equation (1).
Using "time" equation is the STANDARD method of solving such problems.
It is simple, logical, straightforward, economic and robust (works in standard way for any input data).
Going in this way, you will never make a mistake - the logic of the method
prevents you of making mistakes.
From this lesson, learn on how to write, how to use and how to solve a "time" equation.
To see many other similar solved problems, look into the lessons
- Had a car move faster it would arrive sooner
- How far do you live from school?
- Earthquake waves
- Time equation: HOW TO use, HOW TO write and HOW TO solve it
in this site.
/\/\/\/\/\/\/\/
As I do it in many other cases, I will ignore the notice from @greenestamps.
The method of discussion, which he uses, is well known trick.
It is called DEMAGOGY.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Solving the problem using the time equation, as shown by the other tutor, is a perfectly good method; and it is probably the USUAL method. That other tutor likes to make pronouncements that a certain method is the "STANDARD" method, suggesting that you should always solve that particular kind of problem by that method.
I consistently disagree with her on that subject. You should use whatever method you find that gives the right answer, and that you find easy to use.
This kind of problem is one of those where I find a less common method more to my liking; I can solve this kind of problem much faster by a method that does not involve writing and solving an algebraic equation.
(1) The ratio of the two speeds is 30:45 = 2:3.
(2) Since the distances are the same, the ratio of times at the two speeds is 3:2.
(3) Therefore, 3/5 of the 8 hours was at the lower speed of 30mph, and 2/5 of the 8 hours was at the higher speed of 45mph.
The distance is then determined using the speed and time for either direction:
going: (3/5) of (8) hours at (30mph) = (3/5)(8)(30) = 144 miles
returning: (2/5) of (8) hours at (45mph) = (2/5)(8)(45) = 144 miles
|
|
|
