Question 1151683: Please help me to solve this question:
Assume that the random variable X is normally distributed, with mean=31.5 and standard deviation=1.4. Compute the probability P(X<28).
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! there are online calculators that allow you to solve this directly without having to figure out what the z-score is.
one such calculator can be found at https://www.omnicalculator.com/statistics/normal-distribution
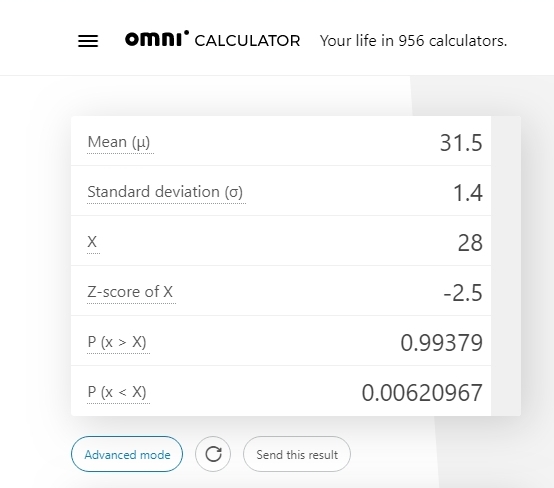
i used this calculator and input a mean of 31.5 and a standard deviation of 1.4 and an X value of 28.
the calculator gave me p(X < 28), shown as p(x < X).
it also gave me p(X > 28), shown as p(x > X).
it also gave me the z-score, shown as -2.5.
here's what the output looked like.
i also used another normal distribution calculator that gives you the result and also shows you a visualization of that looks like under the normal distribution curve.
that calculator can be found at http://davidmlane.com/hyperstat/z_table.html
with this calculator, you can enter z-score of -2.5 with a mean of 0 and a standard deviation of 1, or you can enter a raw score of 28 with a mean of 31.5 and a standard deviation of 1.4
here's what the results from that calculator look like.
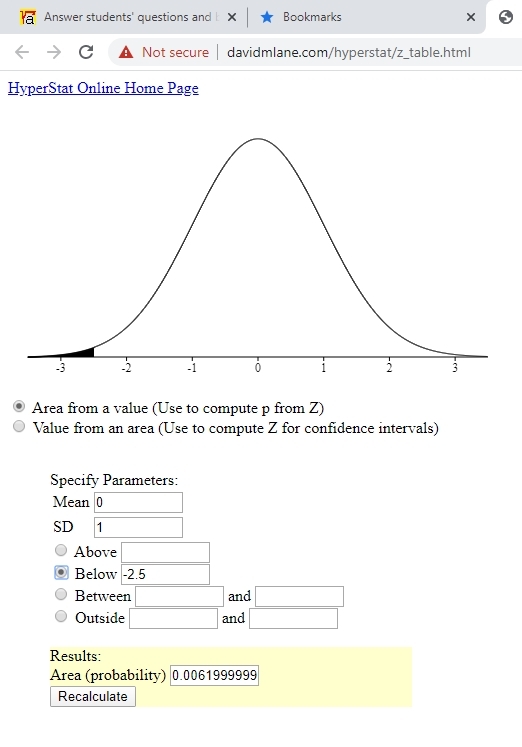

note that the probability of getting a score < 28 using this calculator was slightly different than the probability using the omni calculator.
this will happen when using different calculator because they may not all have the same underlying assumptions regarding interpolation of results between known value and / or different assumption regarding intermediate rounding of results.
for practical purposes, probability estimates rounded from 2 to 4 decimal places should be all that you need.
the omni calculator will give you the z-score if you give it the mean of 31.5 and an X value of 28 and a standard deviation of 1.4
the david m. lane calculator will give you the result if you give it the mean of 31.5 and an X value of 28 and a standard deviation of 1.4, but it won't give you the z-score.
to find the z-score, you would need to use the z-score formula.
that formula is z = (x - m) / s
z is the z-score
x is the raw score
m is the mean
s is the standard deviation, in this case.
using that formula, you would get:
z = (28 - 31.5) / 1.4
solve for z to get z = -2.5
the omni calculator give me the same result that i get from using my TI-84 Plus calculator, with less effort.
bottom line:
omni is pretty good.
there is also an advance mode that can give you the probability between two values, either from 2 z-scores or from 2 raw scores.
for your purposes, p(x < X) where X = 28 would be .0062 rounded to 4 decimal places.
|
|
|