Question 1151680: Joe's annual income has been increasing each year by the same dollar amount. The first year his income was $19 comma 900, and the 4th year his income was $23 comma 800. In which year was his income $ 31 comma 600 question mark
Found 2 solutions by rfer, ikleyn:
Answer by rfer(16322)   (Show Source): (Show Source):
Answer by ikleyn(52930)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From the post by @rfer you may conclude that the answer is "at the 9-th year".
But do not hurry --- it would be wrong (!)
Read my solution below.
You start count that income from the first year:
 , ,  , ,  , . . . , , . . . ,  .
The first term of this sequence is $19900.
It is arithmetic sequence, and its common difference is 1300, as @rfer correctly determined in his post.
Therefore, you can write .
The first term of this sequence is $19900.
It is arithmetic sequence, and its common difference is 1300, as @rfer correctly determined in his post.
Therefore, you can write
 = 1300 + (n-1)*1300.
You want to find "n" in a way that
31600 = 1300 + (n-1)*1300.
It gives you
n - 1 = = 1300 + (n-1)*1300.
You want to find "n" in a way that
31600 = 1300 + (n-1)*1300.
It gives you
n - 1 = 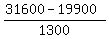 = = 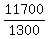 = 9.
Hence, n = 9+1 = 10.
ANSWER. "At which year ?" ---- at the 10-th year. = 9.
Hence, n = 9+1 = 10.
ANSWER. "At which year ?" ---- at the 10-th year.
So, the correct answer is "at the 10-th year"; or 9 years after the 1-st year.
Solved.
From my post learn that not only calculations, but the entire conception of the solution and the answer itself
should be presented accurately -- if you want high scores.
------------------
For introductory lessons on arithmetic progressions see
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|